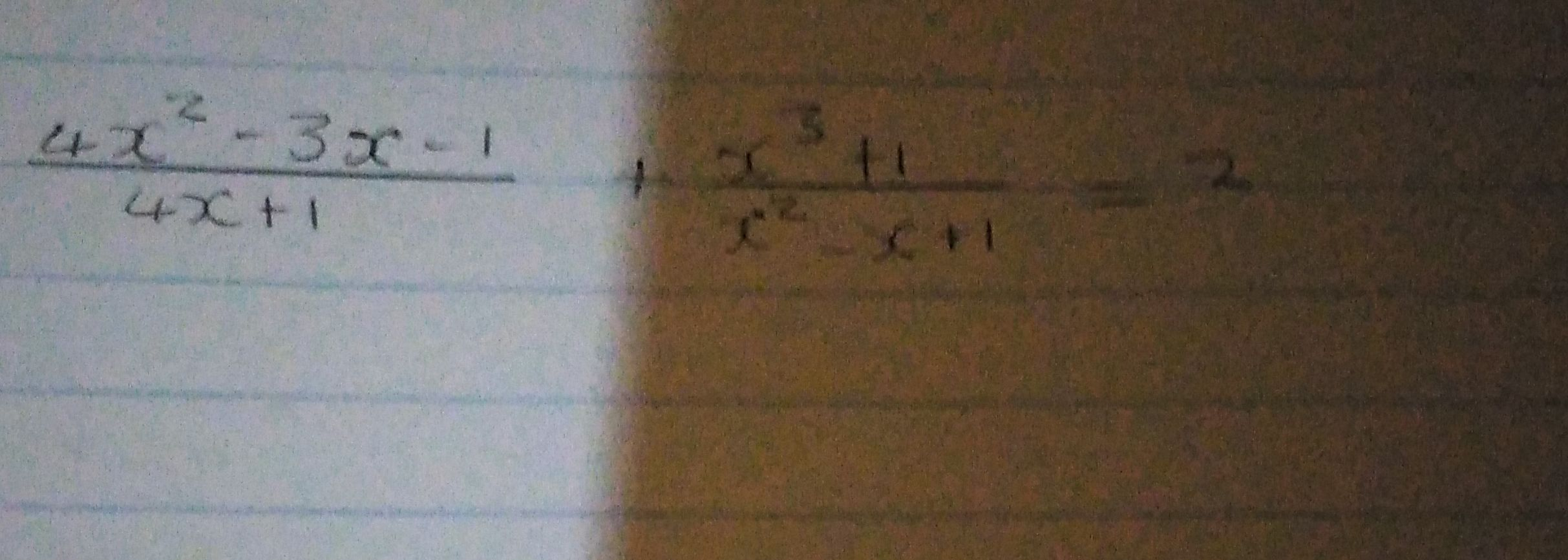AI tutor
Full solution
Q. Find the values of .
- Identify Terms and Denominator: First, let's identify the individual terms of the equation and understand that we need to find a common denominator to combine the fractions on the left side of the equation.
- Find Common Denominator: The common denominator for the two fractions and would be their product, . We will multiply both the numerator and denominator of each fraction by the necessary terms to achieve this common denominator.
- Multiply First Fraction: Multiply the first fraction by to get .
- Multiply Second Fraction: Multiply the second fraction by to get .
- Combine Fractions: Now, we will add the two fractions together since they have the same denominator. This gives us:
- Expand First Numerator: We need to expand the numerators of both fractions before adding them. Let's start with the first numerator . We will use the distributive property (FOIL) to expand this product.
- Expand Second Numerator: Expanding gives us .
- Add Expanded Numerators: Combining like terms in the expanded expression gives us .
- Combine Like Terms: Now let's expand the second numerator using the distributive property.
- Eliminate Denominator: Expanding gives us .
- Expand Right Side: Now we add the expanded numerators together: + .
- Combine Like Terms Right Side: Combining like terms gives us .
- Distribute Right Side: Now we have the combined fraction as .
- Set Equation to Zero: To solve for , we need to get rid of the denominator. We can do this by multiplying both sides of the equation by the denominator, which gives us .
- Subtract Right Side: Now we need to expand the right side of the equation: .
- Quartic Equation Error: Expanding the right side gives us .
- Quartic Equation Error: Expanding the right side gives us .Combining like terms on the right side gives us .
- Quartic Equation Error: Expanding the right side gives us . Combining like terms on the right side gives us . Distributing the across the terms on the right side gives us .
- Quartic Equation Error: Expanding the right side gives us . Combining like terms on the right side gives us . Distributing the across the terms on the right side gives us . Now we have the equation .
- Quartic Equation Error: Expanding the right side gives us . Combining like terms on the right side gives us . Distributing the across the terms on the right side gives us . Now we have the equation . We need to bring all terms to one side to set the equation to zero: .
- Quartic Equation Error: Expanding the right side gives us . Combining like terms on the right side gives us . Distributing the across the terms on the right side gives us . Now we have the equation . We need to bring all terms to one side to set the equation to zero: . Subtracting the terms on the right from the left gives us .
- Quartic Equation Error: Expanding the right side gives us . Combining like terms on the right side gives us . Distributing the across the terms on the right side gives us . Now we have the equation . We need to bring all terms to one side to set the equation to zero: . Subtracting the terms on the right from the left gives us . This is a quartic equation, and solving it algebraically can be very complex. We would typically use numerical methods or graphing to find the roots. However, there is a mistake in the previous steps. The derivative of is not as stated in Step of the full solution. The correct derivative should be multiplied by the derivative of the inner function , which is . Therefore, the correct derivative of is . This means there is a math error in the full solution provided.