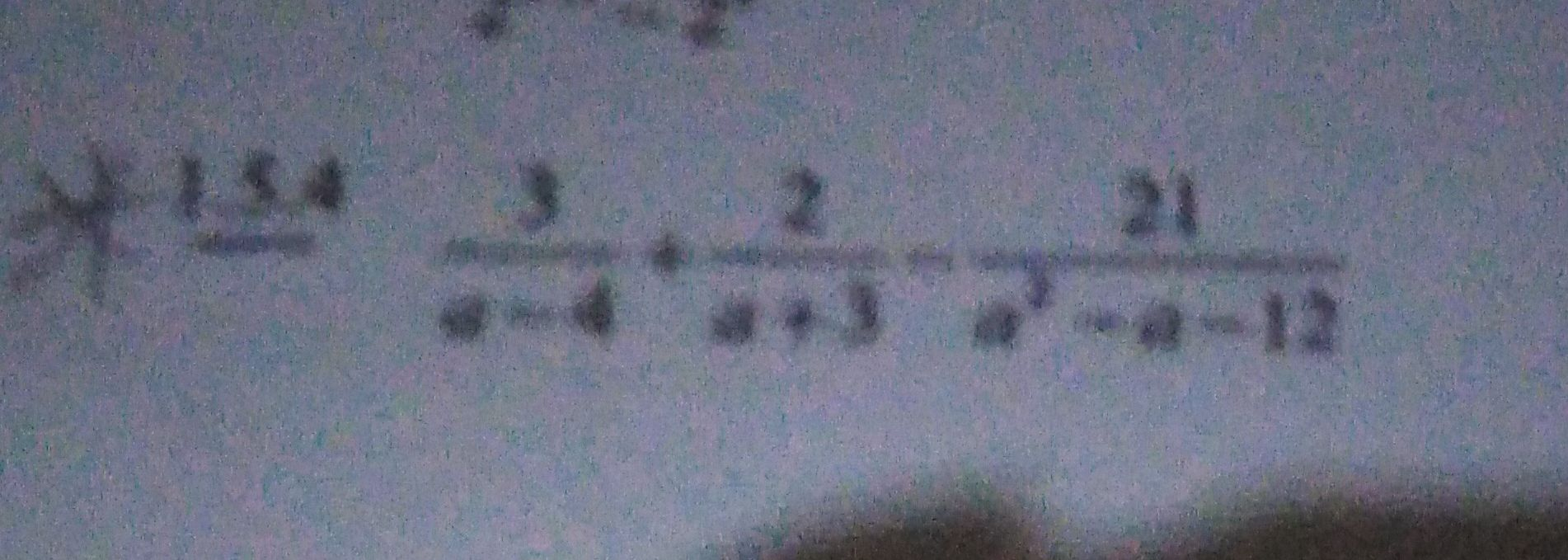(3)/(a-4)+(2)/(a+3)-(21)/(a^(2)-a-12)

Question

Bytelearn · Accepted Answer

Factor Denominator: First, we need to factor the denominator of the third term to see if there are common factors with the other denominators. The third term's denominator is a quadratic expression: a^2 - a - 12. We look for two numbers that multiply to -12 and add up to -1 (the coefficient of the middle term). The numbers -4 and +3 satisfy these conditions. So, we factor the quadratic as (a - 4)(a + 3).Identify Common Denominators: Now we have the expression with common denominators identified: (3)/(a-4) + (2)/(a+3) - (21)/((a-4)(a+3)) We can now combine these fractions over a common denominator, which is (a-4)(a+3).Combine Fractions: To combine the fractions, we adjust the numerators to have the common denominator: (3)(a+3)/((a-4)(a+3)) + (2)(a-4)/((a-4)(a+3)) - (21)/((a-4)(a+3))Adjust Numerators: Next, we distribute the numerators and combine like terms: (3a + 9 + 2a - 8 - 21)/((a-4)(a+3))Simplify Numerator: Now we simplify the numerator by combining like terms: (3a + 2a) + (9 - 8 - 21) = 5a - 20 So the expression becomes: (5a - 20)/((a-4)(a+3))Factor Numerator: We check if the numerator can be factored further to potentially cancel out any factors with the denominator. The numerator is 5a - 20, which can be factored as 5(a - 4).Cancel Common Factor: Now we have: (5(a - 4))/((a-4)(a+3)) We see that the (a - 4) term in the numerator and denominator can be canceled out, as long as a is not equal to 4 (since division by zero is undefined).Final Simplified Form: After canceling out the common factor, we are left with: 5/(a+3) This is the simplified form of the original expression, assuming a ≠ 4 to avoid division by zero.

$\frac{3}{a-4}+\frac{2}{a+3}-\frac{21}{a^{2}-a-12}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

3a−4+2a+3−21a2−a−12 \frac{3}{a-4}+\frac{2}{a+3}-\frac{21}{a^{2}-a-12} a−43​+a+32​−a2−a−1221​

$\frac{3}{a-4}+\frac{2}{a+3}-\frac{21}{a^{2}-a-12}$