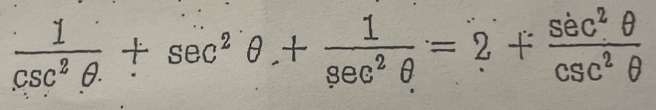Prove that (1)/(csc^(2)theta)+sec^(2)theta+(1)/(sec^(2)theta)=2+(sec^(2)theta)/(csc^(2)theta)

Question

Prove that  (1)/(csc^(2)theta)+sec^(2)theta+(1)/(sec^(2)theta)=2+(sec^(2)theta)/(csc^(2)theta)

Bytelearn · Accepted Answer

Recall Definitions: First, let's recall the definitions of the secant and cosecant functions in terms of sine and cosine: sec(theta) = 1/cos(theta) csc(theta) = 1/sin(theta) We will use these definitions to rewrite the given expression in terms of sine and cosine.Rewrite First Term: Now, let's rewrite the first term (1)/(csc^(2)theta) as sin^(2)theta: (1)/(csc^(2)theta) = (1)/((1/sin(theta))^2) = sin^(2)thetaRewrite Third Term: Next, we rewrite the third term (1)/(sec^(2)theta) as cos^(2)theta: (1)/(sec^(2)theta) = (1)/((1/cos(theta))^2) = cos^(2)thetaRewrite Right Side: Now, let's rewrite the right side of the equation (sec^(2)theta)/(csc^(2)theta) as (1/cos^(2)theta)/(1/sin^(2)theta), which simplifies to sin^(2)theta/cos^(2)theta, which is tan^(2)theta: (sec^(2)theta)/(csc^(2)theta) = (1/cos^(2)theta)/(1/sin^(2)theta) = sin^(2)theta/cos^(2)theta = tan^(2)thetaRewrite Entire Equation: We can now rewrite the entire equation using these trigonometric identities: sin^(2)theta + sec^(2)theta + cos^(2)theta = 2 + tan^(2)thetaApply Pythagorean Identity: We know from the Pythagorean identity that sin^(2)theta + cos^(2)theta = 1. Let's apply this identity to simplify the left side of the equation: 1 + sec^(2)theta = 2 + tan^(2)thetaSubstitute Identity: Another Pythagorean identity tells us that sec^(2)theta = 1 + tan^(2)theta. Let's substitute this into the equation: 1 + (1 + tan^(2)theta) = 2 + tan^(2)thetaSimplify Left Side: Now, simplify the left side of the equation by combining like terms: 2 + tan^(2)theta = 2 + tan^(2)thetaVerify Equality: We see that both sides of the equation are equal, which means the original expression is an identity.

Prove that $\frac{1}{\csc^{2}\theta}+\sec^{2}\theta+\frac{1}{\sec^{2}\theta}=2+\frac{\sec^{2}\theta}{\csc^{2}\theta}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Prove that 1csc⁡2θ+sec⁡2θ+1sec⁡2θ=2+sec⁡2θcsc⁡2θ\frac{1}{\csc^{2}\theta}+\sec^{2}\theta+\frac{1}{\sec^{2}\theta}=2+\frac{\sec^{2}\theta}{\csc^{2}\theta}csc2θ1​+sec2θ+sec2θ1​=2+csc2θsec2θ​

Prove that $\frac{1}{\csc^{2}\theta}+\sec^{2}\theta+\frac{1}{\sec^{2}\theta}=2+\frac{\sec^{2}\theta}{\csc^{2}\theta}$