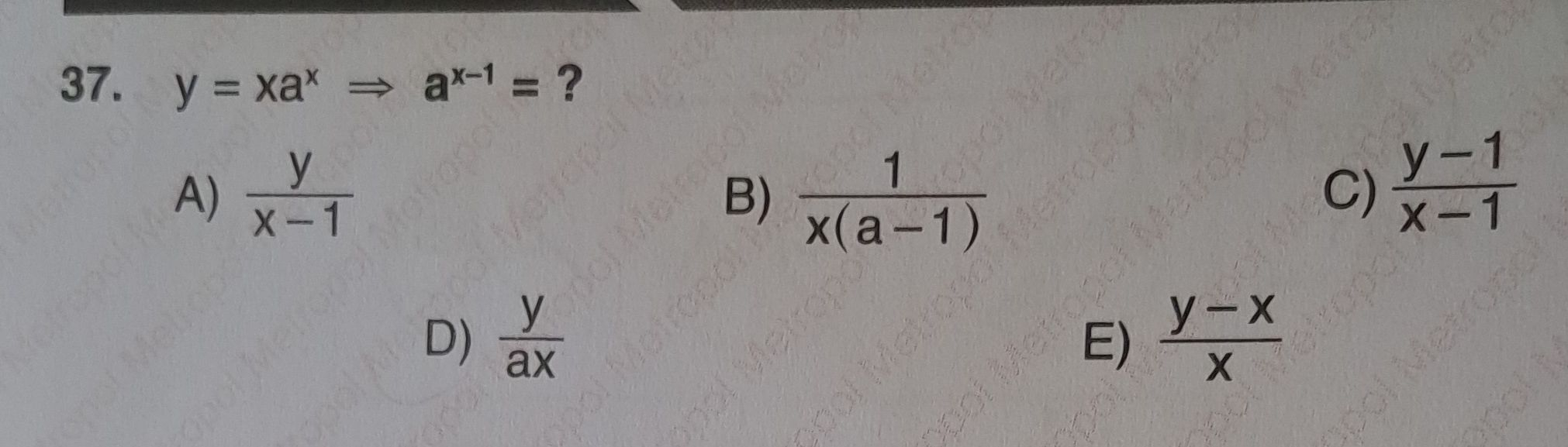AI tutor
Full solution
Q. . ?A) B) C) D) E)
- Isolate a^x: We are given the equation . We want to express in terms of and . To do this, we can start by isolating on one side of the equation.
- Express a^(x): Next, we need to express . We can use the property of exponents that states .So, we substitute with from the previous step.
- Simplify the Expression: Now, we simplify the expression by dividing by .
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help