Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

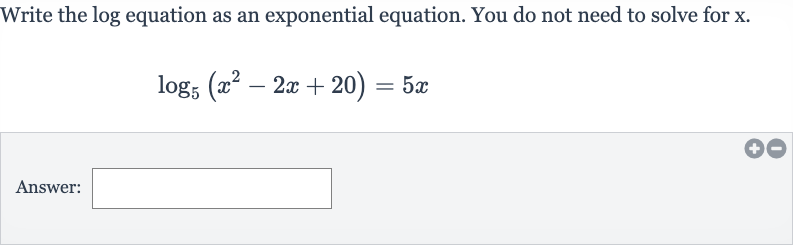
Write the log equation as an exponential equation. You do not need to solve for
x.

log_(5)(x^(2)-2x+20)=5x
Answer:

Write the log equation as an exponential equation. You do not need to solve for $\mathrm{x}$ . $\newline$ $\log _{5}\left(x^{2}-2 x+20\right)=5 x$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Convert between exponential and logarithmic form: all bases

Full solution

Q. Write the log equation as an exponential equation. You do not need to solve for

\mathrm{x}

.

\newline

\log _{5}\left(x^{2}-2 x+20\right)=5 x

\newline

Answer:

Identify components: Identify the base $b$ , the argument $x$ , and the exponent $y$ in the logarithmic equation. $\newline$ The logarithmic equation is given as $\log_{5}(x^{2}-2x+20)=5x$ . Here, the base $b$ is $5$ , the argument $x$ is $x^{2}-2x+20$ , and the exponent $y$ is $5x$ .
Convert to exponential form: Convert the logarithmic equation to its equivalent exponential form. $\newline$ Using the definition of a logarithm, we can convert the equation $\log_{5}(x^{2}-2x+20)=5x$ to its exponential form by raising the base to the power of the exponent to get the argument. This gives us $5^{5x} = x^{2}-2x+20$ .
Write corresponding equation: Write down the exponential equation that corresponds to the given logarithmic equation. $\newline$ The exponential equation that corresponds to $\log_{5}(x^{2}-2x+20)=5x$ is $5^{5x} = x^{2}-2x+20$ .

More problems from Convert between exponential and logarithmic form: all bases

Question

Convert the exponential equation in logarithmic form.

\newline

9^3 = 729

Posted 4 months ago

Question

Convert the exponential equation in logarithmic form.

\newline

e^4 \approx 54.598

Posted 4 months ago

Question

Write the logarithmic equation in exponential form.

\newline

\log_{10}100 = 2

\newline

10^2 = \underline{\hspace{2em}}

Posted 9 months ago

Question

Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.

\newline

\frac{\ln (e)}{10} =

Posted 4 months ago

Question

Rewrite as a quotient of two common logarithms. Write your answer in simplest form.

\newline

\log_3 33 =

Posted 9 months ago

Question

Evaluate. Round your answer to the nearest thousandth.

\newline

\log_{5}50 =

Posted 9 months ago

Question

Which property of logarithms does this equation demonstrate?

\newline

\log_3 3 + \log_3 6 = \log_3 18

\newline

\newline

\text{Product Property}

\newline

\text{Power Property}

\newline

\text{Quotient Property}

Posted 5 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log(uv)

\newline

Posted 9 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log v^7

\newline

Posted 9 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of base-

6

logarithms or multiples of base-

6

logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log_6 w^6

\newline

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant