Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

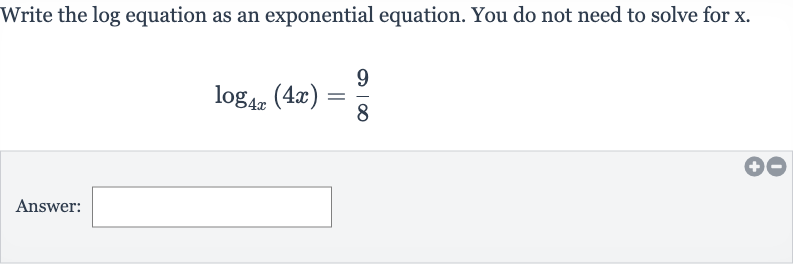
Write the log equation as an exponential equation. You do not need to solve for
x.

log_(4x)(4x)=(9)/(8)
Answer:

Write the log equation as an exponential equation. You do not need to solve for $\mathrm{x}$ . $\newline$ $\log _{4 x}(4 x)=\frac{9}{8}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Quotient property of logarithms

Full solution

Q. Write the log equation as an exponential equation. You do not need to solve for

\mathrm{x}

.

\newline

\log _{4 x}(4 x)=\frac{9}{8}

\newline

Answer:

Understand basic logarithmic form: Understand the basic form of a logarithmic equation and how to convert it to an exponential equation. $\newline$ The basic form of a logarithmic equation is $\log_b(a) = c$ , which can be rewritten as an exponential equation $b^c = a$ . $\newline$ In our case, we have $\log_{(4x)}(4x) = \frac{9}{8}$ . To convert this to an exponential equation, we need to use the base of the logarithm $(4x)$ and raise it to the power of the right-hand side of the equation $\left(\frac{9}{8}\right)$ to get the argument of the logarithm $(4x)$ .
Convert to exponential equation: Convert the logarithmic equation to an exponential equation using the base and the argument. $\newline$ Using the base $(4x)$ and the right-hand side of the equation $\left(\frac{9}{8}\right)$ , we write the exponential equation as $(4x)^{\left(\frac{9}{8}\right)} = 4x$ .

More problems from Quotient property of logarithms

Question

x

\newline

5^x=1

\newline

\newline

Write your answer in simplest form.

Posted 5 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

Posted 4 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

Posted 5 months ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 8 months ago

Question

x

\newline

7 = 9^x

\newline

Round your answer to the nearest thousandth.

Posted 4 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 7 months ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 9 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 7 months ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 4 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6x

\newline

f(x) = 6^x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 4 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant