AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Write the following as an exponential expression.
Full solution
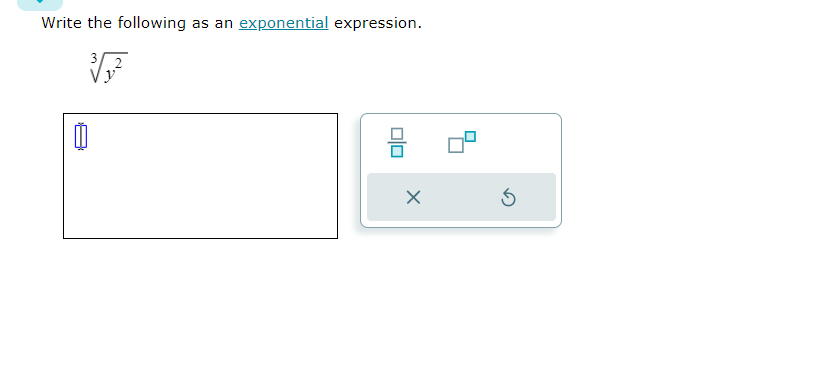
Q. Write the following as an exponential expression.
- Identify Components: Identify the components of the expression.The expression is the cube root of squared. This involves a radical expression with an index of , since it is a cube root, and an exponent of , because it is squared.
- Convert to Exponential: Convert the radical expression to an exponential expression.The cube root of a number can be expressed as that number raised to the power of . Therefore, the cube root of squared is squared raised to the power of .
- Apply Power Rule: Apply the power to a power rule.When you raise a power to another power, you multiply the exponents. In this case, raised to the power of is .
- Perform Exponent Multiplication: Perform the multiplication of the exponents.Multiply by to get . So, squared raised to the power of is .
More problems from Write an equation from words
QuestionGet tutor help
