Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Graph
-27 x+18 y=54.

Graph $-27x+18y=54$ .

View step-by-step help

View step-by-step help

Solve one-step equations with whole numbers

Full solution

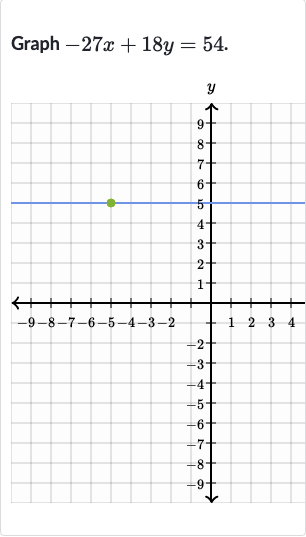
Q. Graph

-27x+18y=54

.

Writing the equation in slope-intercept form: To graph the equation $-27x + 18y = 54$ , we first need to write it in slope-intercept form, which is $y = mx + b$ , where $m$ is the slope and $b$ is the y-intercept.
Isolating y on one side of the equation: We can start by isolating y on one side of the equation. To do this, we can add $27x$ to both sides of the equation: $\newline$ $-27x + 18y + 27x = 54 + 27x$ $\newline$ This simplifies to: $\newline$ $18y = 27x + 54$
Solving for y: Next, we divide every term by $18$ to solve for y: $\newline$ $(\frac{18y}{18}) = (\frac{27x}{18}) + \frac{54}{18}$ $\newline$ This simplifies to: $\newline$ $y = (\frac{3}{2})x + 3$
Identifying the slope and y-intercept: Now that we have the equation in slope-intercept form, we can identify the slope and y-intercept. The slope $m$ is $\frac{3}{2}$ , and the y-intercept $b$ is $3$ .
Plotting the y-intercept: To graph the equation, we start by plotting the y-intercept $(0,3)$ on the y-axis.
Finding another point using the slope: Next, we use the slope to find another point. Starting from the $y$ -intercept, we move $3$ units up (since the slope is positive) and $2$ units to the right (the denominator of the slope). This gives us a second point on the graph.
Drawing the graph: With two points plotted, we can draw a straight line through them to represent the graph of the equation $y = \frac{3}{2}x + 3$ .

More problems from Solve one-step equations with whole numbers

Question

Write the sentence as an equation.

\newline

138

is equal to the quotient of

w

30

\newline

/

) if you want to use a division sign.

\newline

Posted 3 months ago

Question

\newline

(\frac{2}{7})x= -14

\newline

x =

Posted 4 months ago

Question

(\frac{8}{5})x= 32

Posted 4 months ago

Question

\newline

2+2

\newline

Posted 4 days ago

Question

\newline

48.5-0.434=

Posted 4 months ago

Question

\newline

96.7-0.163=

Posted 4 months ago

Question

\newline

4.43-0.283=

Posted 4 months ago

Question

\newline

3.05-0.338=

Posted 4 months ago

Question

\newline

6.168-0.432=

Posted 4 months ago

Question

\begin{array}{l}y+6=5(x-4) \\ y=\square\end{array}

Posted 4 hours ago