Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Write the expression below as a single logarithm in simplest form. 2log_(b)3-log_(b)9 Answer: log_(b)(◻)

Write the expression below as a single logarithm in simplest form.\newline2log⁡b3−log⁡b9 2 \log _{b} 3-\log _{b} 9 \newlineAnswer: log⁡b(□) \log _{b}(\square)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Quotient property of logarithmsright chevron icon

Full solution

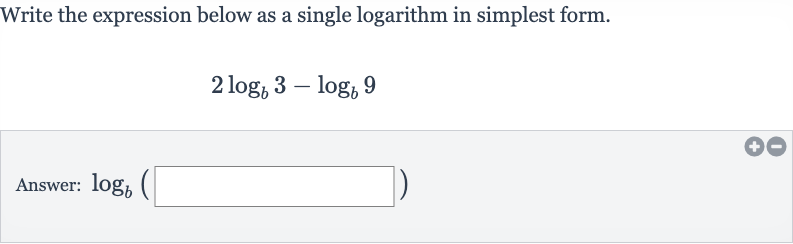
Q. Write the expression below as a single logarithm in simplest form.\newline2log⁡b3−log⁡b9 2 \log _{b} 3-\log _{b} 9 \newlineAnswer: log⁡b(□) \log _{b}(\square)
  1. Identify Properties: Identify the properties used to combine the logarithms.\newlineThe expression given is 2log⁡b3−log⁡b92\log_{b}3 - \log_{b}9. To combine these logarithms into a single logarithm, we will use the power property and the subtraction property of logarithms.\newlinePower Property: log⁡b(Pk)=k⋅log⁡b(P)\log_b(P^k) = k \cdot \log_b(P)\newlineSubtraction Property: log⁡b(P)−log⁡b(Q)=log⁡b(PQ)\log_b(P) - \log_b(Q) = \log_b\left(\frac{P}{Q}\right)
  2. Apply Power Property: Apply the power property to the first term.\newlineThe first term is 2log⁡b32\log_{b}3, which can be rewritten using the power property as log⁡b(32)\log_{b}(3^2).\newlineSo, 2log⁡b32\log_{b}3 becomes log⁡b(32)\log_{b}(3^2) or log⁡b(9)\log_{b}(9).
  3. Combine Logarithms: Combine the two logarithms using the subtraction property.\newlineNow we have log⁡b(9)\log_{b}(9) from the first term and −log⁡b9-\log_{b}9 from the second term. Using the subtraction property, we can combine these into a single logarithm:\newlinelog⁡b(9)−log⁡b9=log⁡b(99)\log_{b}(9) - \log_{b}9 = \log_{b}(\frac{9}{9}).
  4. Simplify Expression: Simplify the expression inside the logarithm.\newlineThe expression inside the logarithm is 99\frac{9}{9}, which simplifies to 11.\newlineSo, log⁡b(99)\log_{b}\left(\frac{9}{9}\right) becomes log⁡b(1)\log_{b}(1).
  5. Recognize Identity: Recognize the logarithmic identity.\newlineThe logarithm of 11 to any base is always 00.\newlineTherefore, log⁡b(1)=0\log_{b}(1) = 0.

More problems from Quotient property of logarithms

Question
Write the exponential equation in logarithmic form.\newline93=7299^3 = 729\newlinelog⁡□729=3\log_\square 729 = 3
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the exponential equation in logarithmic form.\newlinee4≈54.598e^4 \approx 54.598\newlineln⁡____≈4\ln\_\_\_\_ \approx 4
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the logarithmic equation in exponential form.\newlinelog⁡10100=2\log_{10}100 = 2\newline102=‾10^2 = \underline{\hspace{2em}}
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.\newlineln⁡(e)10=\frac{\ln (e)}{10} = ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Rewrite as a quotient of two common logarithms. Write your answer in simplest form.\newlinelog⁡333=\log_3 33 = ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate. Round your answer to the nearest thousandth.\newlinelog⁡550=\log_{5}50 = ____
Get tutor helpright-arrow

Posted 3 months ago

Question
Which property of logarithms does this equation demonstrate? \newlinelog⁡33+log⁡36=log⁡318\log_3 3 + \log_3 6 = \log_3 18\newlineChoices:\newline(A) Product Property\text{Product Property}\newline(B) Power Property\text{Power Property}\newline(C) Quotient Property\text{Quotient Property}
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡(uv)\log(uv)\newline_____
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡v7\log v^7 \newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of base-66 logarithms or multiples of base-66 logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡6w6\log_6 w^6\newline______
Get tutor helpright-arrow

Posted 3 months ago

View all (63)