Full solution
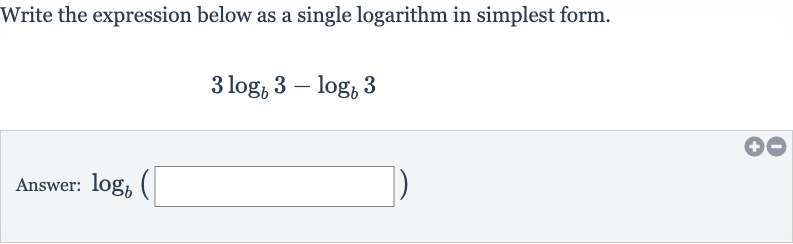
Q. Write the expression below as a single logarithm in simplest form.Answer:
- Identify Properties: Identify the properties of logarithms that can be applied.We have the expression . We can use the power rule of logarithms to rewrite the first term, which states that .
- Apply Power Rule: Apply the power rule to the first term.Using the power rule, we can rewrite as .
- Simplify Exponent: Simplify the exponent.Calculate to simplify the expression.So, becomes .
- Combine Logarithms: Combine the logarithms.Now we have . We can use the quotient rule of logarithms, which states that , to combine these into a single logarithm.
- Apply Quotient Rule: Apply the quotient rule. Using the quotient rule, we combine and into .
- Simplify Fraction: Simplify the fraction inside the logarithm.Calculate to simplify the expression inside the logarithm.So, becomes .