Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Write the expression below as a single logarithm in simplest form. log_(b)4-log_(b)4 Answer: log_(b)(◻)

Write the expression below as a single logarithm in simplest form.\newlinelog⁡b4−log⁡b4 \log _{b} 4-\log _{b} 4 \newlineAnswer: log⁡b(□) \log _{b}(\square)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Quotient property of logarithmsright chevron icon

Full solution

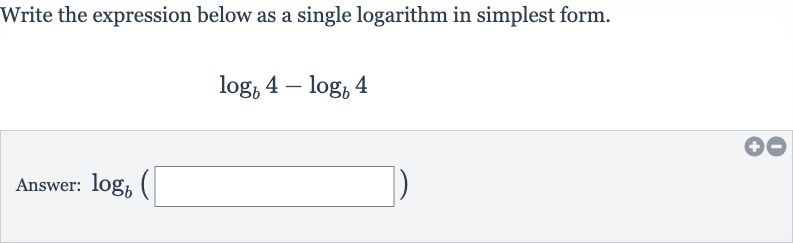
Q. Write the expression below as a single logarithm in simplest form.\newlinelog⁡b4−log⁡b4 \log _{b} 4-\log _{b} 4 \newlineAnswer: log⁡b(□) \log _{b}(\square)
  1. Identify Property: Identify the property used to combine the logarithms.\newlineThe expression log⁡b4−log⁡b4\log_{b}4 - \log_{b}4 involves the subtraction of two logarithms with the same base and the same argument.\newlineThe property that applies here is that the logarithm of any number minus itself is 00.
  2. Apply Property: Apply the property to combine the logarithms.\newlineSince log⁡b4\log_{b}4 and log⁡b4\log_{b}4 are the same, their difference is zero.\newlinelog⁡b4−log⁡b4=0\log_{b}4 - \log_{b}4 = 0
  3. Write Single Logarithm: Write the expression as a single logarithm.\newlineThe expression 00 can be written as log⁡b1\log_{b}1 because the logarithm of 11 to any base is 00.\newlineTherefore, log⁡b4−log⁡b4=log⁡b1\log_{b}4 - \log_{b}4 = \log_{b}1

More problems from Quotient property of logarithms

Question
Write the exponential equation in logarithmic form.\newline93=7299^3 = 729\newlinelog⁡□729=3\log_\square 729 = 3
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the exponential equation in logarithmic form.\newlinee4≈54.598e^4 \approx 54.598\newlineln⁡____≈4\ln\_\_\_\_ \approx 4
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the logarithmic equation in exponential form.\newlinelog⁡10100=2\log_{10}100 = 2\newline102=‾10^2 = \underline{\hspace{2em}}
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.\newlineln⁡(e)10=\frac{\ln (e)}{10} = ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Rewrite as a quotient of two common logarithms. Write your answer in simplest form.\newlinelog⁡333=\log_3 33 = ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate. Round your answer to the nearest thousandth.\newlinelog⁡550=\log_{5}50 = ____
Get tutor helpright-arrow

Posted 3 months ago

Question
Which property of logarithms does this equation demonstrate? \newlinelog⁡33+log⁡36=log⁡318\log_3 3 + \log_3 6 = \log_3 18\newlineChoices:\newline(A) Product Property\text{Product Property}\newline(B) Power Property\text{Power Property}\newline(C) Quotient Property\text{Quotient Property}
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡(uv)\log(uv)\newline_____
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡v7\log v^7 \newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of base-66 logarithms or multiples of base-66 logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡6w6\log_6 w^6\newline______
Get tutor helpright-arrow

Posted 3 months ago

View all (63)