Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Write an exponential function in the form
y=ab^(x) that goes through the points
(0,14) and
(7,1792).
Answer:

Write an exponential function in the form $y=a b^{x}$ that goes through the points $(0,14)$ and $(7,1792)$ . $\newline$ Answer:

View step-by-step help

View step-by-step help

Convert between exponential and logarithmic form: all bases

Full solution

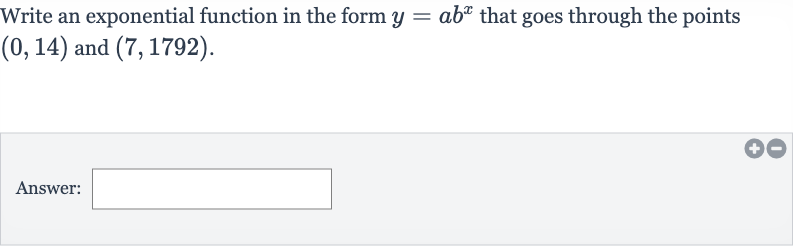
Q. Write an exponential function in the form

y=a b^{x}

that goes through the points

(0,14)

and

(7,1792)

.

\newline

Answer:

Find a Value: We need to find the values of $a$ and $b$ for the exponential function $y=ab^{x}$ that passes through the points $(0,14)$ and $(7,1792)$ . We will use the first point $(0,14)$ to find the value of $a$ . Substitute $x=0$ and $y=14$ into the equation $y=ab^{x}$ . $b$ $0$ Since any number raised to the power of $b$ $1$ is $b$ $2$ , we have: $b$ $3$ Therefore, $b$ $4$ .
Use First Point: Now we will use the second point $(7,1792)$ to find the value of $b$ . Substitute $x=7$ , $y=1792$ , and $a=14$ into the equation $y=ab^{x}$ . $1792 = 14 \times b^7$ To solve for $b$ , we divide both sides by $14$ : $1792 / 14 = b^7$ $b$ $0$ Now we need to find the $b$ $1$ th root of $b$ $2$ to solve for $b$ . $b$ $4$ Calculating the $b$ $1$ th root of $b$ $2$ gives us: $b$ $7$
Use Second Point: We should check if $b \approx 2$ is a correct approximation by raising $2$ to the power of $7$ and see if it equals $128$ . $\newline$ $2^7 = 128$ $\newline$ Since $2^7$ indeed equals $128$ , our value for $b$ is correct.
Check Approximation: Now that we have both $a$ and $b$ , we can write the exponential function. $a = 14$ and $b = 2$ , so the function is: $y = 14 \times 2^{x}$

More problems from Convert between exponential and logarithmic form: all bases

Question

Write the exponential equation in logarithmic form.

\newline

9^3 = 729

\newline

\log_\square 729 = 3

Posted 2 months ago

Question

Write the exponential equation in logarithmic form.

\newline

e^4 \approx 54.598

\newline

\ln\_\_\_\_ \approx 4

Posted 2 months ago

Question

Write the logarithmic equation in exponential form.

\newline

\log_{10}100 = 2

\newline

10^2 = \underline{\hspace{2em}}

Posted 2 months ago

Question

Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.

\newline

\frac{\ln (e)}{10} =

Posted 2 months ago

Question

Rewrite as a quotient of two common logarithms. Write your answer in simplest form.

\newline

\log_3 33 =

Posted 2 months ago

Question

Evaluate. Round your answer to the nearest thousandth.

\newline

\log_{5}50 =

Posted 2 months ago

Question

Which property of logarithms does this equation demonstrate?

\newline

\log_3 3 + \log_3 6 = \log_3 18

\newline

\newline

\text{Product Property}

\newline

\text{Power Property}

\newline

\text{Quotient Property}

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log(uv)

\newline

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log v^7

\newline

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of base-

6

logarithms or multiples of base-

6

logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log_6 w^6

\newline

Posted 2 months ago