Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

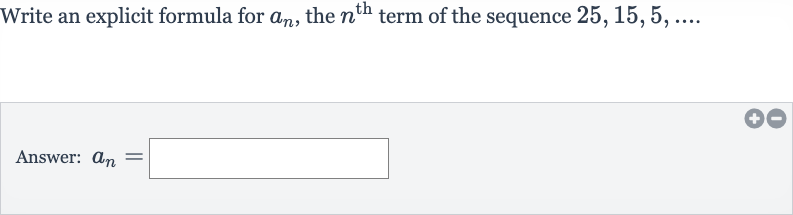
Write an explicit formula for a_(n), the n^("th ") term of the sequence 25,15,5,dots Answer: a_(n)=

Write an explicit formula for an a_{n} , the nth  n^{\text {th }} term of the sequence 25,15,5,… 25,15,5, \ldots \newlineAnswer: an= a_{n}=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Write equations of cosine functions using propertiesright chevron icon

Full solution

Q. Write an explicit formula for an a_{n} , the nth  n^{\text {th }} term of the sequence 25,15,5,… 25,15,5, \ldots \newlineAnswer: an= a_{n}=
  1. Identify Arithmetic Sequence: The given sequence is 25,15,5,…25, 15, 5, \ldots which is an arithmetic sequence because the difference between consecutive terms is constant.
  2. Find Common Difference: To find the common difference dd, subtract the second term from the first term: d=15−25=−10d = 15 - 25 = -10.
  3. Use Arithmetic Sequence Formula: The first term of the sequence a1a_1 is 2525. The nnth term of an arithmetic sequence is given by the formula an=a1+(n−1)da_n = a_1 + (n - 1)d.
  4. Substitute Values: Substitute the values of a1a_1 and dd into the formula: an=25+(n−1)(−10)a_n = 25 + (n - 1)(-10).
  5. Simplify Formula: Simplify the formula: an=25−10n+10a_n = 25 - 10n + 10.
  6. Final Explicit Formula: Combine like terms to get the final explicit formula: an=35−10na_n = 35 - 10n.

More problems from Write equations of cosine functions using properties

Question
Find an equation for a sinusoidal function that has period 2π2\pi, amplitude 11, and contains the point (π,−1)\left(\pi, -1\right). \newlineWrite your answer in the form f(x)=Acos⁡(Bx+C)+Df(x)=A\cos(Bx+C)+D, where AA, BB, CC, and DD are real numbers.\newline f(x)=f(x)=
Get tutor helpright-arrow

Posted 7 months ago

Question
Find an equation for a sinusoidal function that has period 2π2\pi, amplitude 11, and contains the point (−π2,−1)\left(-\frac{\pi}{2},-1\right). Write your answer in the form f(x)=Asin⁡(Bx+C)+Df(x) = A\sin(Bx + C) + D, where AA, BB, CC, and DD are real numbers. `f(x)` =______
Get tutor helpright-arrow

Posted 9 months ago

Question
Find an equation for a sinusoidal function that has period 2π2\pi, amplitude 11, and contains the point (0,−1)(0,-1). \newlineWrite your answer in the form f(x)=Acos⁡(Bx+C)+Df(x) = A\cos(Bx + C) + D, where AA, BB, CC, and DD are real numbers. \newlinef(x)=f(x) = _____
Get tutor helpright-arrow

Posted 8 months ago

Question
Franklin Middle School is having a canned food drive. In Mr. Lao's class, Mr. Lao brought 1010 cans of food, and each student brought 22 cans. In Ms. Roger's class, Ms. Rogers did not bring any cans, but each student brought 33 cans of food. Write two equations in slope-intercept form to represent the number of cans of food for each class yy in terms of the number of students xx.
Get tutor helpright-arrow

Posted 8 months ago

Question
Franklin Middle School is having a canned food drive. In Mr. Lao's class, Mr. Lao brought 1010 cans of food, and each student brought 22 cans. In Ms. Roger's class, Ms. Rogers did not bring any cans, but each student brought 33 cans of food. Write two equations in slope-intercept form to represent the number of cans of food for each class yy in terms of the number of students xx.
Get tutor helpright-arrow

Posted 8 months ago

Question
Kris is wrapping Christmas lights around the railing that runs around three sides of his square porch If one side of his porch is 1212 feet long, and each strand of his Christmes lights will wrap around a 7070-inch length of the railing, what is the minimum number of strands Kris needs to completely wrap the porch railing?\newlineA) 66\newlineB) 77\newlineC) 88\newlineD) 99
Get tutor helpright-arrow

Posted 8 months ago

Question
Kris is wrapping Christmas lights around the railing that runs around three sides of his square porch If one side of his porch is 1212 feet long, and each strand of his Christmas lights will wrap around a 7070-inch length of the railing, what is the minimum number of strands Kris needs to completely wrap the porch railing?\newlineA) 66\newlineB) 77\newlineC) 88\newlineD) 99
Get tutor helpright-arrow

Posted 8 months ago

Question
For a given input value b b , the function f f outputs a value a a to satisfy the following equation.\newline4a+7b=−52 4a+7b=-52 \newlineWrite a formula for f(b) f(b) in terms of b b .\newlinef(b)=□ f(b)=\square
Get tutor helpright-arrow

Posted 6 months ago

Question
For a given input value xx, the function gg outputs a value yy to satisfy the following equation.\newline−4x−6=−5y+2-4x-6=-5y+2\newlineWrite a formula for g(x)g(x) in terms of xx.\newlineg(x)=□g(x)=\square
Get tutor helpright-arrow

Posted 10 months ago

Question
For a given input value aa, the function ff outputs a value bb to satisfy the following equation.\newline−3a+6b=a+4b-3a+6b=a+4b\newlineWrite a formula for f(a)f(a) in terms of aa.\newlinef(a)=□f(a)=\square
Get tutor helpright-arrow

Posted 10 months ago

View all (68)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant