AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
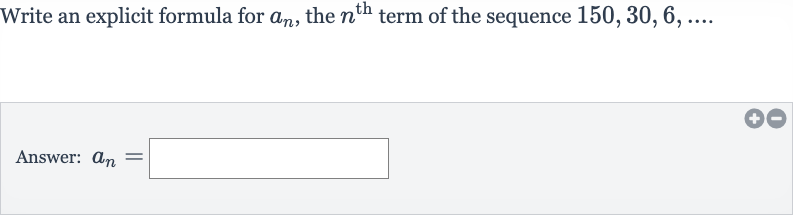
Write an explicit formula for , the term of the sequence .Answer:
Full solution
Q. Write an explicit formula for , the term of the sequence .Answer:
- Identify Pattern: Identify the pattern in the sequence.The sequence is Each term is divided by to get the next term. This is a geometric sequence with a common ratio of
- Determine First Term: Determine the first term of the sequence.The first term of the sequence is .
- Find Common Ratio: Determine the common ratio of the sequence.The common ratio is the factor by which we multiply each term to get the next term. In this case, .
- Write Explicit Formula: Write the explicit formula for the th term of a geometric sequence.The explicit formula for the th term of a geometric sequence is .
- Substitute Values: Substitute the values of and into the formula..
