Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

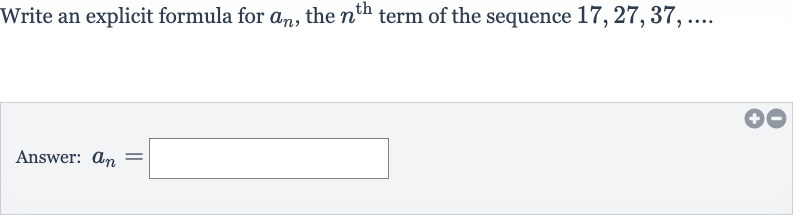
Write an explicit formula for
a_(n), the
n^("th ") term of the sequence
17,27,37,dots.
Answer:
a_(n)=

Write an explicit formula for $a_{n}$ , the $n^{\text {th }}$ term of the sequence $17,27,37, \ldots$ . $\newline$ Answer: $a_{n}=$

View step-by-step help

View step-by-step help

Evaluate an exponential function

Full solution

Q. Write an explicit formula for

a_{n}

, the

n^{\text {th }}

term of the sequence

17,27,37, \ldots

.

\newline

Answer:

a_{n}=

Calculate Common Difference: To find the explicit formula for the $n$ th term of the sequence, we first need to determine the common difference between consecutive terms. We can do this by subtracting the first term from the second term. $\newline$ Calculation: $27 - 17 = 10$
Find nth Term Formula: The common difference is $10$ . This means that each term is $10$ more than the previous term. Since the first term is $17$ , the nth term can be found by starting with $17$ and adding the common difference ( $10$ ) multiplied by $(n - 1)$ times. $\newline$ Calculation: $a_n = 17 + 10(n - 1)$
Simplify nth Term Formula: Now we simplify the formula for the nth term. $\newline$ Calculation: $a_n = 17 + 10n - 10$ $\newline$ Calculation: $a_n = 10n + 7$

More problems from Evaluate an exponential function

Question

Use the following function rule to find

f(2)

\newline

f(x) = 11 \cdot (9)^x + 8

\newline

f(2) =

Posted 3 months ago

Question

Raymond works for a pharmaceutical company that is testing the effectiveness of a new medication. He gave one of the study participants

400

milligrams of the medication, and he knows the amount remaining in the participant's body will decrease by a factor of

1/3

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the amount of medication,

y

, remaining in the participant's body after

x

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

\newline

Posted 3 months ago

Question

100

bacteria doubles in size every

60

hours. What will the population be

180

hours from now?

\newline

Posted 2 months ago

Question

Charlotte opened a savings account and deposited

\$800.00

as principal. The account earns

8\%

interest, compounded annually. What is the balance after

10

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

\newline

Posted 3 months ago

Question

Bob rented a car for a flat fee of `$150` and an additional `$10` per day. Write a linear function that represents the total cost,

f(x)

x

Posted 4 months ago

Question

Sally purchased a laptop for `$800` and has to pay a service fee of `$20` for each day until it is delivered. Write a linear function to represent the total cost,

h(x)

x

Posted 4 months ago

Question

\$1,000

in a savings account with a daily interest rate of

0.1\%

. Write an exponential function to represent the total amount,

s(x)

, in his account after

x

Posted 4 months ago

Question

A=2450+740 s

\newline

The total amount,

A

, in thousands of dollars, of scholarship money given out by a college throughout its history at a time of

s

semesters after the summer of the year

2000

is given by the equation. What was the total amount of scholarship money, in thousands of dollars, given out by the college up to the summer of the year

2000

Posted 1 month ago

Question

T=235+980 d

\newline

T

, in newton-meters, on a diving board with a

100

kilogram weight placed

d

meters from the diving board's fulcrum is given by the equation. How much torque in newton-meters is on the diving board when the weight is placed at the fulcrum?

Posted 2 months ago

Question

R=42-0.7 t

\newline

Quinn returned home one summer's day to find it extremely hot. He turned the air conditioner on, and the room's temperature began decreasing at a constant rate. The given equation shown gives the room's temperature,

R

, in degrees Celsius,

t

minutes after Quinn turned on the air conditioner. What was the room's temperature, in degrees Celsius, when Quinn returned home?

Posted 1 month ago