AI tutor
Full solution
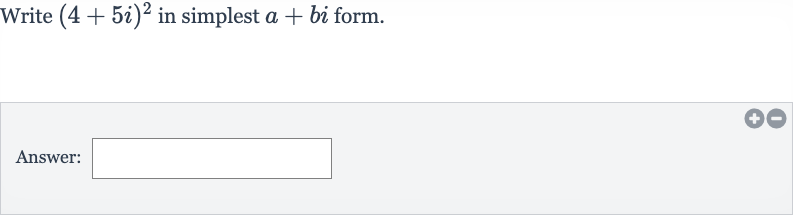
Q. Write in simplest form.Answer:
- Square Complex Number: To find the simplest form of , we need to square the complex number . We use the formula . Let's calculate it: .
- Calculate Real Part: First, we calculate the real part of the expression: .
- Calculate Imaginary Part: Next, we calculate the imaginary part without the : , so the imaginary part is .
- Calculate i Squared Part: Now, we calculate the i squared part: . Since , we have .
- Combine Real and Imaginary Parts: We combine the real part and the imaginary parts: (from step ) + (from step ) - (from step ).So, .
- Final Simplified Form: Finally, we combine the real parts and keep the imaginary part separate: + = . This is the simplest form of ^{}.