AI tutor
Full solution
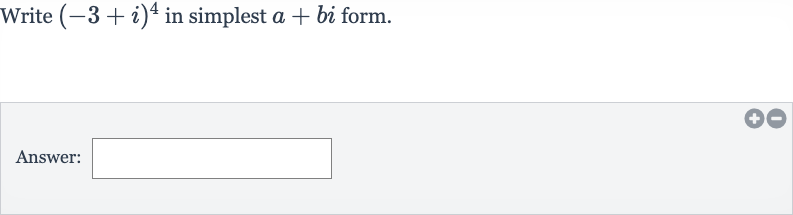
Q. Write in simplest form.Answer:
- Recognize Complex Number: To solve , we first need to recognize that we are raising a complex number to the fourth power. We can start by raising to simplify the expression step by step.
- Square to Simplify: Now we need to square the result of to get . Since , we replace with to get:
- Square Result for : We have now expressed in the simplest form, which is .