AI tutor
Full solution
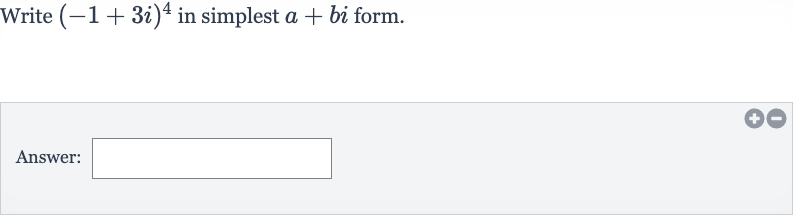
Q. Write in simplest form.Answer:
- Calculate First Square: To solve , we will first calculate the square of and then square the result again to get the fourth power.(-1+3i) \times (-1+3i) = (-1)^2 + 2\times(-1)\times3i + (3i)^2\(\newline= 1 - 6i - 9(i^2)\)Since , we replace with .
- Replace with : Now we need to square the result to get the fourth power of .
Again, we replace with .