AI tutor
Full solution
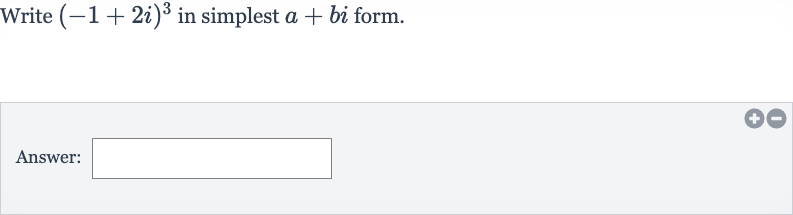
Q. Write in simplest form.Answer:
- Calculate Square: To solve , we will first calculate the square of and then multiply the result by again.. Since , we replace with ..
- Multiply by : Now we have the square of , which is . We will multiply this result by to find the cube.Again, we replace with .