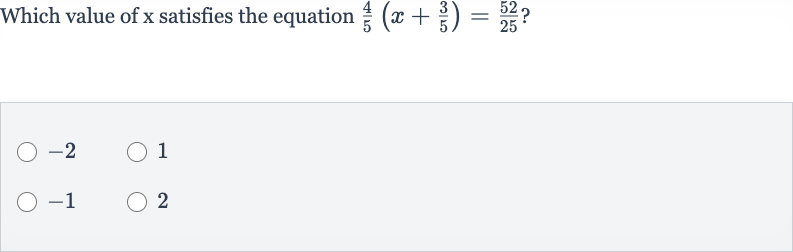AI tutor
Full solution
Q. Which value of satisfies the equation ?
- Solve Equation: First, we need to solve the equation for .
- Multiply by : Multiply both sides of the equation by to isolate the term with .\left(\frac{\(5\)}{\(4\)}\right)\left(\frac{\(4\)}{\(5\)}\right)(x+\left(\frac{\(3\)}{\(5\)}\right)) = \left(\frac{\(5\)}{\(4\)}\right)\left(\frac{\(52\)}{\(25\)}\right)
- Simplify Equation: Simplify both sides of the equation. \(x + \left(\frac{3}{5}\right) = \left(\frac{5\times52}{4\times25}\right)
- Calculate Right Side: Calculate the right side of the equation.
- Simplify Fraction: Simplify the fraction on the right side of the equation.
- Subtract (\frac{\(3\)}{\(5\)}): Further simplify the fraction on the right side of the equation.\[x + \left(\frac{3}{5}\right) = \frac{13}{5}\]
- Combine Fractions: Subtract \((\frac{3}{5}) from both sides of the equation to solve for .
- Calculate Final Value: Combine the fractions on the right side of the equation.
- Simplify Fraction: Calculate the final value of .
- Simplify Fraction: Calculate the final value of . Simplify the fraction to find the value of .
More problems from Find limits involving trigonometric functions
QuestionGet tutor help
QuestionGet tutor help