Full solution

Q. Find

\lim _{x \rightarrow \infty} \frac{x+1}{x^{2}+1}

\newline

Choose

1

answer:

\newline

(A)

1

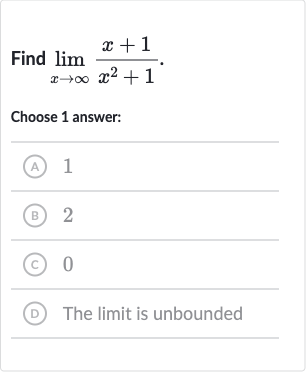
\newline

(B)

2

\newline

(C)

0

\newline

(D) The limit is unbounded

Analyze Behavior of Functions: We are asked to find the limit of the function $(x+1)/(x^2+1)$ as $x$ approaches infinity. To do this, we will analyze the behavior of the numerator and the denominator separately as $x$ grows without bound.
Degree of Polynomials: The degree of the polynomial in the numerator is $1$ (since the highest power of $x$ is $x^1$ ), and the degree of the polynomial in the denominator is $2$ (since the highest power of $x$ is $x^2$ ). When the degree of the denominator is higher than the degree of the numerator, the limit as $x$ approaches infinity is $0$ .
Divide Numerator and Denominator: To formally show this, we can divide both the numerator and the denominator by $x^2$ , the highest power of $x$ in the denominator. This will give us: $\newline$ $\lim_{x \rightarrow \infty}\left(\frac{x}{x^2} + \frac{1}{x^2}\right)/\left(1 + \frac{1}{x^2}\right).$
Simplify Expression: Simplifying the expression inside the limit, we get: $\lim_{x \rightarrow \infty}\left(\frac{1}{x} + \frac{1}{x^2}\right)/\left(1 + \frac{1}{x^2}\right)$ .
Apply Limit as x Approaches Infinity: As $x$ approaches infinity, $\frac{1}{x}$ and $\frac{1}{x^2}$ both approach $0$ . Therefore, the expression simplifies to: $\lim_{x \rightarrow \infty}(0 + 0)/(1 + 0)$ .
Final Limit Calculation: The limit then becomes: $\lim_{x \rightarrow \infty}\frac{0}{1} = 0$ .