AI tutor
Full solution
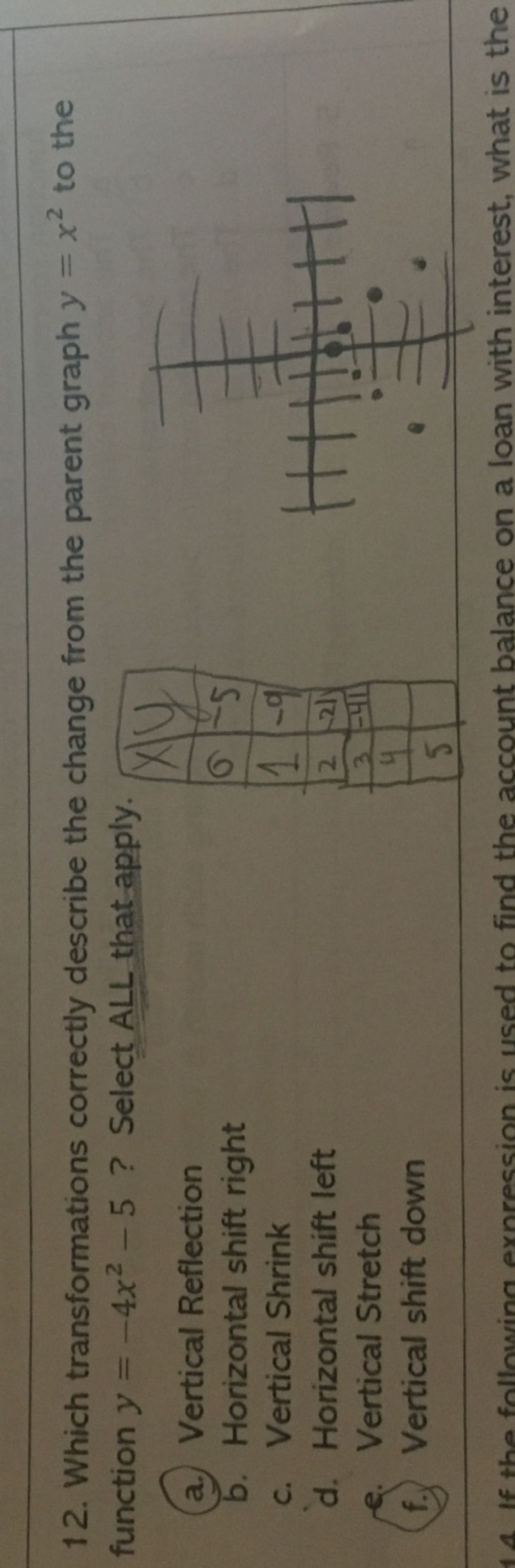
Q. Which transformations correctly describe the change from the parent graph to the function ? Select ALL that apply.a. Vertical Reflectionb. Horizontal shift rightc. Vertical Shrinkd. Horizontal shift lefte. Vertical Stretchf. Vertical shift down
- Analyze Coefficient of : Analyze the coefficient of in both equations. The parent graph has , and the new function has . The coefficient changes from to and flips sign, indicating a Vertical Reflection and a Vertical Shrink by a factor of .
- Check for Horizontal Shifts: Check for any horizontal shifts. The term in both equations does not have any added or subtracted constants inside the parentheses with , which means there are no horizontal shifts.
- Examine Constant Term: Examine the constant term in the new function. The parent graph has no constant term, but the new function has . This indicates a Vertical shift down by units.
More problems from Dilations of functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help