Full solution
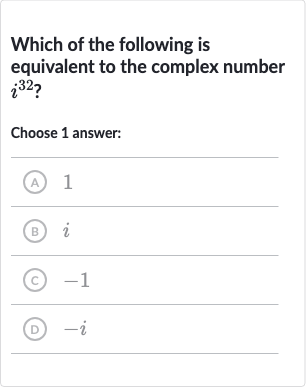
Q. Which of the following is equivalent to the complex number ?Choose answer:(A) (B) (C) (D)
- Understand Powers of i: To find the equivalent of , we need to know the pattern of powers of . The powers of repeat in a cycle of : , , , and . After , the cycle repeats.
- Simplify : Since the powers of repeat every steps, we can simplify by dividing by . The remainder of this division will tell us the equivalent power of within the first cycle of .
- Calculate : Divide by : . Since there is no remainder, is equivalent to , which is .
- Find Equivalent of : We know that . Therefore, .
- Calculate : Calculate : , because any non-zero number raised to any power is itself.
- Conclude : Since , we conclude that is equivalent to .
More problems from Quadratic equation with complex roots
QuestionGet tutor help
QuestionGet tutor help