AI tutor
Full solution
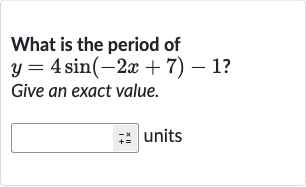
Q. What is the period ofGive an exact value.units
- Identify Sine Function Form: Identify the general form of a sine function and its period.The general form of a sine function is , where the period is given by .
- Substitute Given Values: Substitute the given values into the formula to find the period.Given , we identify . The period is then calculated as .
- Simplify Expression: Simplify the expression to find the exact value of the period. simplifies to . Therefore, the period of the function is units.
More problems from Powers of i
QuestionGet tutor help
QuestionGet tutor help