Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which of the following is equivalent to
(log(t))/(log_(8)(t)) ?
Choose 1 answer:
(A)
log(8)
(B)
log_(8)(t^(2))
(C)
(1)/(log(8))
(D)
(1)/(log_(8)(t^(2)))

Which of the following is equivalent to $\frac{\log (t)}{\log _{8}(t)}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\log (8)$ $\newline$ (B) $\log _{8}\left(t^{2}\right)$ $\newline$ (C) $\frac{1}{\log (8)}$ $\newline$ (D) $\frac{1}{\log _{8}\left(t^{2}\right)}$

View step-by-step help

View step-by-step help

Product property of logarithms

Full solution

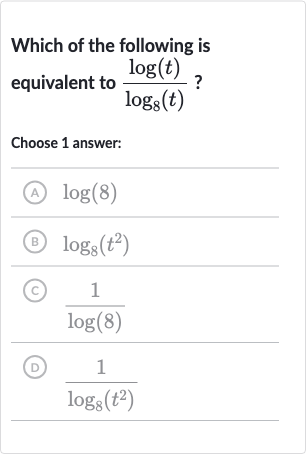
Q. Which of the following is equivalent to

\frac{\log (t)}{\log _{8}(t)}

?

\newline

Choose

1

answer:

\newline

(A)

\log (8)

\newline

(B)

\log _{8}\left(t^{2}\right)

\newline

(C)

\frac{1}{\log (8)}

\newline

(D)

\frac{1}{\log _{8}\left(t^{2}\right)}

Multiply by $\log(8)$ : Simplify the expression by multiplying both numerator and denominator by $\log(8)$ . $\frac{\log(t) \cdot \log(8)}{\frac{\log(t)}{\log(8)} \cdot \log(8)}$
Cancel out $\log(t)$ : Cancel out $\log(t)$ in the numerator and denominator. $\log(8)$

More problems from Product property of logarithms

Question

Write the exponential equation in logarithmic form.

\newline

9^3 = 729

\newline

\log_\square 729 = 3

Posted 2 months ago

Question

Write the exponential equation in logarithmic form.

\newline

e^4 \approx 54.598

\newline

\ln\_\_\_\_ \approx 4

Posted 2 months ago

Question

Write the logarithmic equation in exponential form.

\newline

\log_{10}100 = 2

\newline

10^2 = \underline{\hspace{2em}}

Posted 2 months ago

Question

Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.

\newline

\frac{\ln (e)}{10} =

Posted 2 months ago

Question

Rewrite as a quotient of two common logarithms. Write your answer in simplest form.

\newline

\log_3 33 =

Posted 2 months ago

Question

Evaluate. Round your answer to the nearest thousandth.

\newline

\log_{5}50 =

Posted 2 months ago

Question

Which property of logarithms does this equation demonstrate?

\newline

\log_3 3 + \log_3 6 = \log_3 18

\newline

\newline

\text{Product Property}

\newline

\text{Power Property}

\newline

\text{Quotient Property}

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log(uv)

\newline

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log v^7

\newline

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of base-

6

logarithms or multiples of base-

6

logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log_6 w^6

\newline

Posted 2 months ago