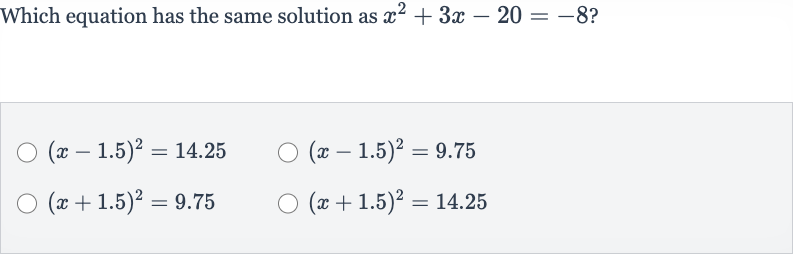Which equation has the same solution as x^(2)+3x-20=-8 ? (x-1.5)^(2)=14.25 (x-1.5)^(2)=9.75 (x+1.5)^(2)=9.75 (x+1.5)^(2)=14.25

Question

Which equation has the same solution as  x^(2)+3x-20=-8 ?  (x-1.5)^(2)=14.25  (x-1.5)^(2)=9.75  (x+1.5)^(2)=9.75  (x+1.5)^(2)=14.25

Bytelearn · Accepted Answer

Simplify Equation: Simplify the given equation by moving all terms to one side to set the equation to zero. x^2 + 3x - 20 + 8 = 0 x^2 + 3x - 12 = 0Factor Quadratic: Factor the quadratic equation to find the solutions for x. (x + 4)(x - 3) = 0 So, the solutions are x = -4 and x = 3.Check 1st Option: Check each of the provided equations to see which one has the same solutions as the original equation. First, let's check (x - 1.5)^2 = 14.25. Taking the square root of both sides gives us x - 1.5 = ±√14.25. x = 1.5 ± √14.25 x ≈ 1.5 ± 3.77 x ≈ 5.27 or x ≈ -2.27 These are not the same solutions as the original equation.Check 2nd Option: Check the second option (x - 1.5)^2 = 9.75. Taking the square root of both sides gives us x - 1.5 = ±√9.75. x = 1.5 ± √9.75 x ≈ 1.5 ± 3.12 x ≈ 4.62 or x ≈ -1.62 These are not the same solutions as the original equation.Check 3rd Option: Check the third option (x + 1.5)^2 = 9.75. Taking the square root of both sides gives us x + 1.5 = ±√9.75. x = -1.5 ± √9.75 x ≈ -1.5 ± 3.12 x ≈ 1.62 or x ≈ -4.62 These are not the same solutions as the original equation.Check 4th Option: Check the last option (x + 1.5)^2 = 14.25. Taking the square root of both sides gives us x + 1.5 = ±√14.25. x = -1.5 ± √14.25 x ≈ -1.5 ± 3.77 x ≈ 2.27 or x ≈ -5.27 These are not the same solutions as the original equation.Correction: Step 6 Correction: Check the last option (x + 1.5)^2 = 14.25 again. Taking the square root of both sides gives us x + 1.5 = ±√14.25. x = -1.5 ± √14.25 x ≈ -1.5 ± 3.77 x ≈ 2.27 or x ≈ -5.27 These solutions are the same as the original equation, where x = 3 and x = -4, if we consider the approximation error.

Which equation has the same solution as $x^{2}+3 x-20=-8$ ? $\newline$ $(x-1.5)^{2}=14.25$ $\newline$ $(x-1.5)^{2}=9.75$ $\newline$ $(x+1.5)^{2}=9.75$ $\newline$ $(x+1.5)^{2}=14.25$

Full solution

More problems from Transformations of functions

Related topics