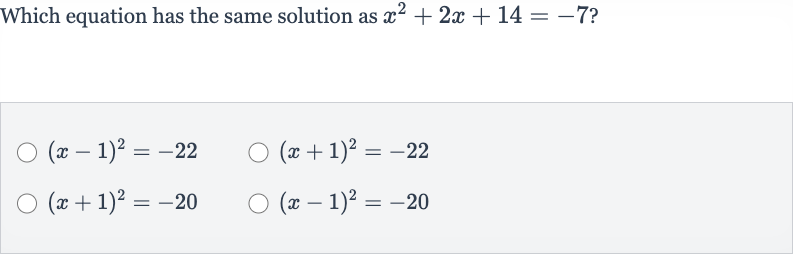Which equation has the same solution as x^(2)+2x+14=-7 ? (x-1)^(2)=-22 (x+1)^(2)=-22 (x+1)^(2)=-20 (x-1)^(2)=-20

Question

Which equation has the same solution as  x^(2)+2x+14=-7 ?  (x-1)^(2)=-22  (x+1)^(2)=-22  (x+1)^(2)=-20  (x-1)^(2)=-20

Bytelearn · Accepted Answer

Simplify Equation: Simplify the given equation by moving all terms to one side to set the equation to zero. x^2 + 2x + 14 = -7 Add 7 to both sides to isolate the quadratic expression. x^2 + 2x + 14 + 7 = 0 x^2 + 2x + 21 = 0Compare with Options: Compare the simplified equation with each of the provided options to find the one that has the same solution. We need to find an equation that, when simplified, will result in x^2 + 2x + 21 = 0.Check Option 1: Simplify the first option and check if it matches the simplified given equation. (x - 1)^2 = -22 Expand the left side: (x - 1)(x - 1) = -22 x^2 - 2x + 1 = -22 Add 22 to both sides: x^2 - 2x + 1 + 22 = 0 x^2 - 2x + 23 = 0 This does not match x^2 + 2x + 21 = 0.Check Option 2: Simplify the second option and check if it matches the simplified given equation. (x + 1)^2 = -22 Expand the left side: (x + 1)(x + 1) = -22 x^2 + 2x + 1 = -22 Add 22 to both sides: x^2 + 2x + 1 + 22 = 0 x^2 + 2x + 23 = 0 This does not match x^2 + 2x + 21 = 0.Check Option 3: Simplify the third option and check if it matches the simplified given equation. (x + 1)^2 = -20 Expand the left side: (x + 1)(x + 1) = -20 x^2 + 2x + 1 = -20 Add 20 to both sides: x^2 + 2x + 1 + 20 = 0 x^2 + 2x + 21 = 0 This matches x^2 + 2x + 21 = 0.Final Match: There is no need to check the fourth option since we have already found a match in the third option. The equation (x + 1)^2 = -20 has the same solution as x^2 + 2x + 21 = 0.

Which equation has the same solution as $x^{2}+2 x+14=-7$ ? $\newline$ $(x-1)^{2}=-22$ $\newline$ $(x+1)^{2}=-22$ $\newline$ $(x+1)^{2}=-20$ $\newline$ $(x-1)^{2}=-20$

Full solution

More problems from Transformations of functions

Related topics

Which equation has the same solution as x2+2x+14=−7 x^{2}+2 x+14=-7 x2+2x+14=−7 ?\newline(x−1)2=−22 (x-1)^{2}=-22 (x−1)2=−22\newline(x+1)2=−22 (x+1)^{2}=-22 (x+1)2=−22\newline(x+1)2=−20 (x+1)^{2}=-20 (x+1)2=−20\newline(x−1)2=−20 (x-1)^{2}=-20 (x−1)2=−20

Which equation has the same solution as $x^{2}+2 x+14=-7$ ? $\newline$ $(x-1)^{2}=-22$ $\newline$ $(x+1)^{2}=-22$ $\newline$ $(x+1)^{2}=-20$ $\newline$ $(x-1)^{2}=-20$