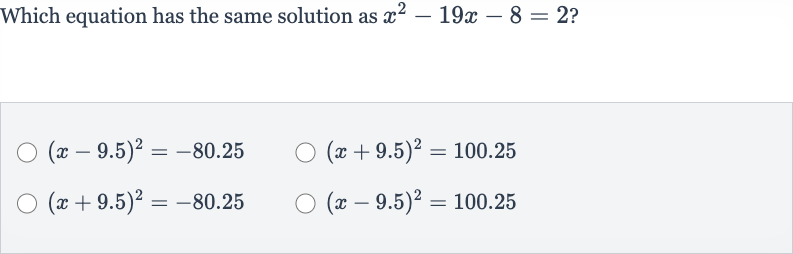AI tutor
Full solution
Q. Which equation has the same solution as ?
- Simplify Equation: Simplify the given equation by moving all terms to one side to set the equation equal to zero.
- Find Vertex Form: Find the vertex form of the quadratic equation. The vertex form is given by , where is the vertex of the parabola.To find , use the formula , where is the coefficient of and is the coefficient of .In this case, and , so .
- Calculate Vertex Coordinates: Calculate the value of by substituting back into the original equation.
- Write Vertex Form Equation: Write the equation in vertex form using the values of and .
- Compare with Choices: Compare the vertex form equation with the given choices to find the one that matches.The correct choice is , which is not listed among the choices provided. However, if we add to both sides of the equation, we get:
- Correct Mistake: Realize that there has been a mistake in the previous step. The correct step should be to add to both sides of the equation to get:This matches one of the given choices.
More problems from Transformations of functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help