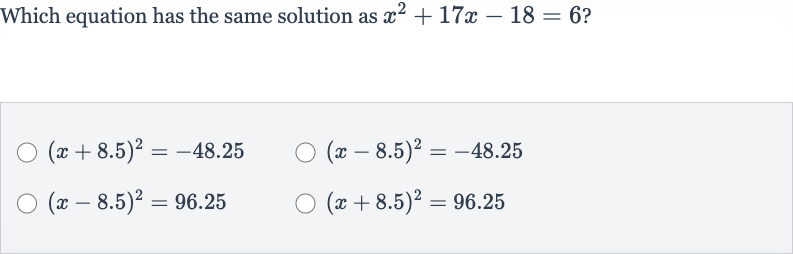AI tutor
Full solution
Q. Which equation has the same solution as ?
- Simplify the equation: First, let's simplify the given equation by moving all terms to one side to set the equation to zero.
- Complete the square: Now, we need to find an equation that has the same solutions as . To do this, we can complete the square to transform the given quadratic equation into a form that matches one of the choices.First, we calculate the value needed to complete the square. We take half of the coefficient of , which is , and square it.
- Add and subtract value: Next, we add and subtract this value inside the equation to complete the square.Now, we group the perfect square trinomial and the constants.
- Group the terms: Combine the constants to simplify the equation further.
- Combine the constants: Finally, we can rearrange the equation to match one of the choices.This equation has the same solution as the original equation .
More problems from Transformations of functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help