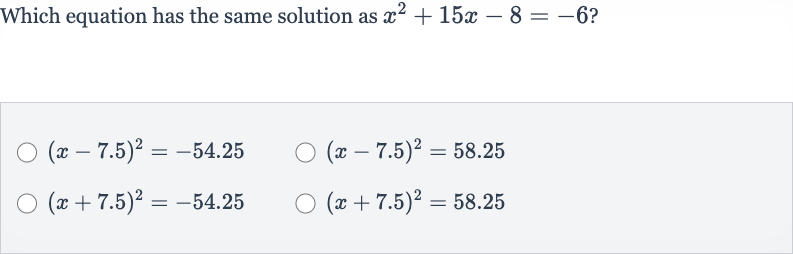Which equation has the same solution as x^(2)+15 x-8=-6 ? (x-7.5)^(2)=-54.25 (x-7.5)^(2)=58.25 (x+7.5)^(2)=-54.25 (x+7.5)^(2)=58.25

Question

Which equation has the same solution as  x^(2)+15 x-8=-6 ?  (x-7.5)^(2)=-54.25  (x-7.5)^(2)=58.25  (x+7.5)^(2)=-54.25  (x+7.5)^(2)=58.25

Bytelearn · Accepted Answer

Add 6 to both sides: Add 6 to both sides of the given equation to set it equal to zero. We start with the equation x^2 + 15x - 8 = -6 and add 6 to both sides to get: x^2 + 15x - 8 + 6 = 0 x^2 + 15x - 2 = 0Complete the square: Complete the square to transform the equation into vertex form. To complete the square, we need to find a value that, when added to both sides of the equation, makes the left side a perfect square trinomial. The value we need to add is (b/2)^2, where b is the coefficient of x. In this case, b = 15, so (b/2)^2 = (15/2)^2 = 225/4. We add 225/4 to both sides of the equation: x^2 + 15x + 225/4 - 2 = 225/4Convert to vertex form: Convert the left side into a perfect square and simplify the right side. We rewrite the left side as a squared binomial and simplify the right side: (x + 15/2)^2 - 2 = 225/4 To simplify the right side, we need to convert -2 into a fraction with the same denominator as 225/4, which is 4. So -2 is -8/4: (x + 15/2)^2 - 8/4 = 225/4 Now we combine the fractions on the right side: (x + 15/2)^2 = 225/4 + 8/4 (x + 15/2)^2 = 233/4Convert to decimal: Convert the fraction on the right side to a decimal to match the answer choices. The fraction 233/4 is equal to 58.25 when converted to a decimal: (x + 15/2)^2 = 58.25Recognize and rewrite: Recognize that 15/2 is equal to 7.5 and rewrite the equation. We can rewrite the equation as: (x + 7.5)^2 = 58.25

Which equation has the same solution as $x^{2}+15 x-8=-6$ ? $\newline$ $(x-7.5)^{2}=-54.25$ $\newline$ $(x-7.5)^{2}=58.25$ $\newline$ $(x+7.5)^{2}=-54.25$ $\newline$ $(x+7.5)^{2}=58.25$

Full solution

More problems from Transformations of functions

Related topics