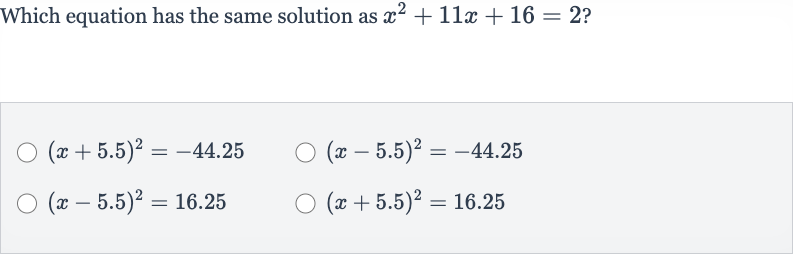Which equation has the same solution as x^(2)+11 x+16=2 ? (x+5.5)^(2)=-44.25 (x-5.5)^(2)=-44.25 (x-5.5)^(2)=16.25 (x+5.5)^(2)=16.25

Question

Which equation has the same solution as  x^(2)+11 x+16=2 ?  (x+5.5)^(2)=-44.25  (x-5.5)^(2)=-44.25  (x-5.5)^(2)=16.25  (x+5.5)^(2)=16.25

Bytelearn · Accepted Answer

Simplify Equation: Simplify the given equation by moving all terms to one side to set the equation to zero. x^2 + 11x + 16 - 2 = 0 x^2 + 11x + 14 = 0Factor Quadratic: Factor the quadratic equation if possible. (x + 7)(x + 2) = 0Solve for x: Solve for x by setting each factor equal to zero. x + 7 = 0 or x + 2 = 0 x = -7 or x = -2Check Solutions: Check the given choices to see which one has the same solutions as the factored equation. We are looking for an equation that has solutions x = -7 and x = -2.Analyze Choice 1: Analyze the first choice. (x + 5.5)^2 = -44.25 This equation cannot have real solutions because the square of a real number cannot be negative.Analyze Choice 2: Analyze the second choice. (x - 5.5)^2 = -44.25 This equation also cannot have real solutions for the same reason as the first choice.Analyze Choice 3: Analyze the third choice. (x - 5.5)^2 = 16.25 Taking the square root of both sides gives us two possible solutions: x - 5.5 = ±4.025 x = 5.5 ± 4.025 x = 9.525 or x = 1.475 These are not the solutions we are looking for.Analyze Choice 4: Analyze the fourth choice. (x + 5.5)^2 = 16.25 Taking the square root of both sides gives us two possible solutions: x + 5.5 = ±4.025 x = -5.5 ± 4.025 x = -1.475 or x = -9.525 These are not the solutions we are looking for.No Matching Solutions: None of the given choices have the same solutions as the original equation x^2 + 11x + 14 = 0.

Which equation has the same solution as $x^{2}+11 x+16=2$ ? $\newline$ $(x+5.5)^{2}=-44.25$ $\newline$ $(x-5.5)^{2}=-44.25$ $\newline$ $(x-5.5)^{2}=16.25$ $\newline$ $(x+5.5)^{2}=16.25$

Full solution

More problems from Transformations of functions

Related topics