AI tutor
Full solution
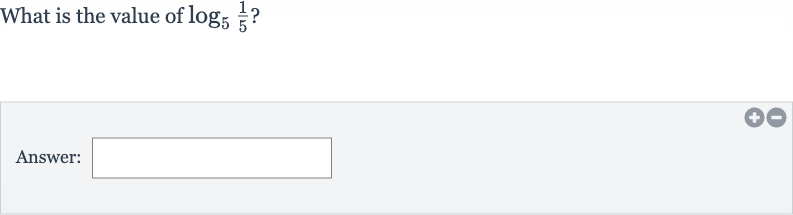
Q. Evaluate.Write your answer in simplest form.
- Identify Base and Argument: Identify the base and the argument of the logarithm.We are given the logarithm , which means we are looking for the power to which must be raised to get .
- Apply Logarithm Definition: Apply the definition of a logarithm.The definition of a logarithm states that if , then . In this case, we want to find such that .
- Recognize Base-Argument Relationship: Recognize the relationship between the base and the argument.Since is (because any number to the negative first power is the reciprocal of that number), we can see that
- Equate Exponents: Equate the exponents.If , then by the property of equality for exponential expressions, must be equal to .
- Conclude Logarithm Value: Conclude the value of the logarithm.Therefore, is equal to .