AI tutor
Full solution
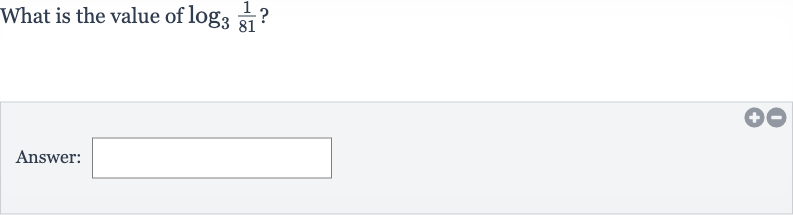
Q. Evaluate.Write your answer in simplest form.
- Recognize base and argument: Recognize the base and the argument of the logarithm. We are dealing with a logarithm with base and the argument is . We need to express as a power of to simplify the logarithm.
- Express as power of : Express as a power of .Since is raised to the power of (), can be written as .
- Apply logarithm definition: Apply the definition of logarithm.Using the fact that , we can write as .
- Write final answer: Write down the final answer.The value of is .