Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

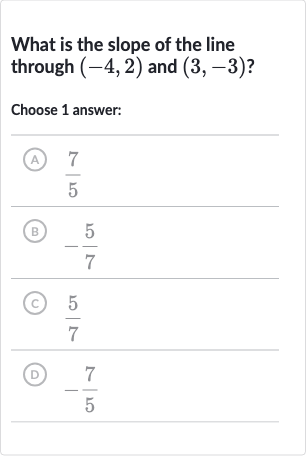
What is the slope of the line through (-4,2) and (3,-3) ? Choose 1 answer: (A) (7)/(5) (B) -(5)/(7) (C) (5)/(7) (D) -(7)/(5)

What is the slope of the line through (−4,2) (-4,2) and (3,−3) (3,-3) ?\newlineChoose 11 answer:\newline(A) 75 \frac{7}{5} \newline(B) −57 -\frac{5}{7} \newline(C) 57 \frac{5}{7} \newline(D) −75 -\frac{7}{5}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Find the slope from two pointsright chevron icon

Full solution

Q. What is the slope of the line through (−4,2) (-4,2) and (3,−3) (3,-3) ?\newlineChoose 11 answer:\newline(A) 75 \frac{7}{5} \newline(B) −57 -\frac{5}{7} \newline(C) 57 \frac{5}{7} \newline(D) −75 -\frac{7}{5}
  1. Identify slope formula: Identify the slope formula.\newlineThe slope of a line is calculated by the difference in the yy-coordinates divided by the difference in the xx-coordinates of two points on the line.\newlineSlope formula: (y2−y1)/(x2−x1)(y_2 - y_1)/(x_2 - x_1)
  2. Substitute given points: Substitute the given points into the slope formula.\newlineWe have the points (−4,2)(-4, 2) and (3,−3)(3, -3). Let's denote (−4,2)(-4, 2) as (x1,y1)(x_1, y_1) and (3,−3)(3, -3) as (x2,y2)(x_2, y_2).\newlineSlope: −3−23−(−4)\frac{-3 - 2}{3 - (-4)}
  3. Calculate change in y: Calculate the change in y y2−y1y_2 - y_1.−3−2-3 - 2 equals −5-5.
  4. Calculate change in x: Calculate the change in xx (x2−x1x_2 - x_1).\newline3−(−4)3 - (-4) equals 77.
  5. Calculate slope: Calculate the slope using the changes in yy and xx.Slope=−57\text{Slope} = \frac{-5}{7}
  6. Simplify slope: Simplify the slope if necessary.\newlineThe slope −57-\frac{5}{7} is already in simplest form and matches one of the given answer choices.

More problems from Find the slope from two points

Question
What is the slope of the line through (−7,−2) (-7,-2) and (−6,7) (-6,7) ?\newlineChoose 11 answer:\newline(A) −19 -\frac{1}{9} \newline(B) −9-9\newline(C) 19 \frac{1}{9} \newline(D) 99
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the slope of the line through (−1,−7) (-1,-7) and (3,9) (3,9) ?\newlineChoose 11 answer:\newline(A) −14 -\frac{1}{4} \newline(B) 44\newline(C) −4-4\newline(D) 14 \frac{1}{4}
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the slope of the line through (6,9) (6,9) and (7,1) (7,1) ?\newlineChoose 11 answer:\newline(A) 88\newline(B) −8-8\newline(C) 18 \frac{1}{8} \newline(D) −18 -\frac{1}{8}
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the slope of the line through (1,0) (1,0) and (3,8) (3,8) ?\newlineChoose 11 answer:\newline(A) 44\newline(B) −4-4\newline(C) −14 -\frac{1}{4} \newline(D) 14 \frac{1}{4}
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the slope of the line through (−7,−8) (-7,-8) and (0,4) (0,4) ?\newlineChoose 11 answer:\newline(A) 127 \frac{12}{7} \newline(B) −712 -\frac{7}{12} \newline(C) −127 -\frac{12}{7} \newline(D) 712 \frac{7}{12}
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the slope of the line through (−1,8) (-1,8) and (3,−4) (3,-4) ?\newlineChoose 11 answer:\newline(A) 33\newline(B) −13 -\frac{1}{3} \newline(C) 13 \frac{1}{3} \newline(D) −3-3
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the slope of the line through (1,−1) (1,-1) and (5,−7) (5,-7) ?\newlineChoose 11 answer:\newline(A) 32 \frac{3}{2} \newline(B) −32 -\frac{3}{2} \newline(C) −23 -\frac{2}{3} \newline(D) 23 \frac{2}{3}
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the slope of the line through (−9,6) (-9,6) and (−3,9) (-3,9) ?\newlineChoose 11 answer:\newline(A) 12 \frac{1}{2} \newline(B) −2-2\newline(C) −12 -\frac{1}{2} \newline(D) 22
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the slope of the line through (2,−2) (2,-2) and (9,3) (9,3) ?\newlineChoose 11 answer:\newline(A) 75 \frac{7}{5} \newline(B) 57 \frac{5}{7} \newline(c) −75 -\frac{7}{5} \newline(D) −57 -\frac{5}{7}
Get tutor helpright-arrow

Posted 3 months ago

Question
I=\int_{−1-1}^{11}\frac{11}{x}\sqrt{\frac{11+x}{11-x}}\ln{\left(\frac{22x^{22}+22x+11}{22x^{22}−2-2x+11}\right)}\,dx
Get tutor helpright-arrow

Posted 11 hours ago

View all (15)