AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Vijay needs to take a taxi, which costs a flat fee of dollars, plus an additional dollars per mile. If Vijay has dollars with him, which inequality shows the number of miles, , he can afford to travel in the taxi?Choose answer:(A) (B) (C) (D)
Full solution
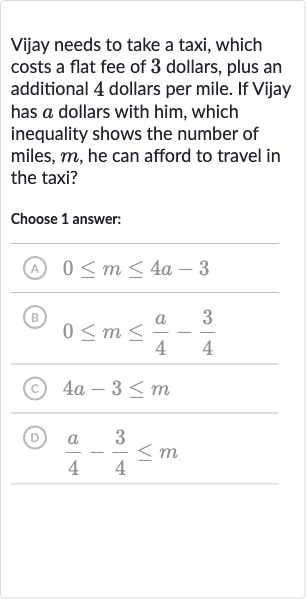
Q. Vijay needs to take a taxi, which costs a flat fee of dollars, plus an additional dollars per mile. If Vijay has dollars with him, which inequality shows the number of miles, , he can afford to travel in the taxi?Choose answer:(A) (B) (C) (D)
- Calculate total cost: The total cost of the taxi ride is the sum of the flat fee and the cost per mile. The flat fee is , and the cost per mile is per mile. So, the total cost for miles is .
- Formulate inequality: Vijay has a \geq + m$.
- Isolate variable: To find the inequality in terms of \(m\), we need to isolate \(m\). We do this by subtracting \(3\) from both sides of the inequality \(a - 3 \geq 4m\).
- Solve for m: Next, we divide both sides of the inequality by \(4\) to solve for \(m\): \((a - 3)/4 \geq m\).
- Flip inequality: Since we want the inequality to show the number of miles \(m\) he can afford, we flip the inequality to \(m \leq (a - 3)/4\).
- Consider non-negativity: We also know that \(m\) cannot be negative, so we have the additional condition that \(m \geq 0\). Combining this with the previous inequality, we get \(0 \leq m \leq \frac{a - 3}{4}\).
- Simplify inequality: Now we simplify the right side of the inequality: \((a - 3)/4 = a/4 - 3/4\). So the inequality becomes \(0 \leq m \leq a/4 - 3/4\).
More problems from One-step inequalities: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help