Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

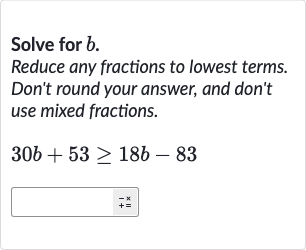
$Solve for b. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions. 30 b+53 >= 18 b-83$

Solve for $b$ . Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions. $\newline$ $30b + 53 \geq 18b - 83$

View step-by-step help

View step-by-step help

Solve multi-step inequalities

Full solution

Q. Solve for

b

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

30b + 53 \geq 18b - 83

Isolate variable $b$ : First, we want to isolate the variable $b$ on one side of the inequality. To do this, we will subtract $18$ b from both sides. $\newline$ $30$ b + $53$ - $18$ b \(0\).\(5\)em] \geq \(18\)b - \(83\) - \(18\)b
Simplify both sides: Now, we simplify both sides of the inequality by combining like terms.\(\newline\)\((30b - 18b) + 53 \geq -83\)\(\newline\)\(12b + 53 \geq -83\)
Isolate \(b\) completely: Next, we want to isolate \(b\) completely. To do this, we will subtract \(53\) from both sides of the inequality.\[12b + 53 - 53 \geq -83 - 53 $12b \geq -136$
Divide both sides: Finally, we divide both sides of the inequality by $12$ to solve for $b$ . $\newline$ $\frac{12b}{12} \geq \frac{-136}{12}$ $\newline$ $b \geq \frac{-136}{12}$
Reduce the fraction: We reduce the fraction $-\frac{136}{12}$ to its lowest terms. $\newline$ $b \geq -11\frac{1}{3}$

More problems from Solve multi-step inequalities

Question

w

\newline

\frac{w}{-1} + 7 > 9

\newline

Posted 6 months ago

Question

u

\newline

6.4u < 3.84 + 6.8u

\newline

\newline

Write your answer with

u

first, followed by an inequality symbol.

\newline

\newline

Posted 6 months ago

Question

t

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

12t - 2 < -5t + 36

Posted 6 months ago

Question

m

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

8m + 95 < -87m + 5

Posted 8 months ago

Question

r

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

35r-21 < -35r+19

Posted 8 months ago

Question

x

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

54x + 64 \geq 49x + 59

Posted 8 months ago

Question

w

.\ Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

53w+13 < 56w+16

Posted 8 months ago

Question

p

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

-7p - 4 > 26p - 94

Posted 8 months ago

Question

d

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

-23d + 81 \leq -98d + 1

Posted 8 months ago

Question

๔

. Dibuje la gráfica de la función logarítmica

f(x)=\log _{2}(x+4)

e indique lo siguiente:

Posted 20 hours ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant