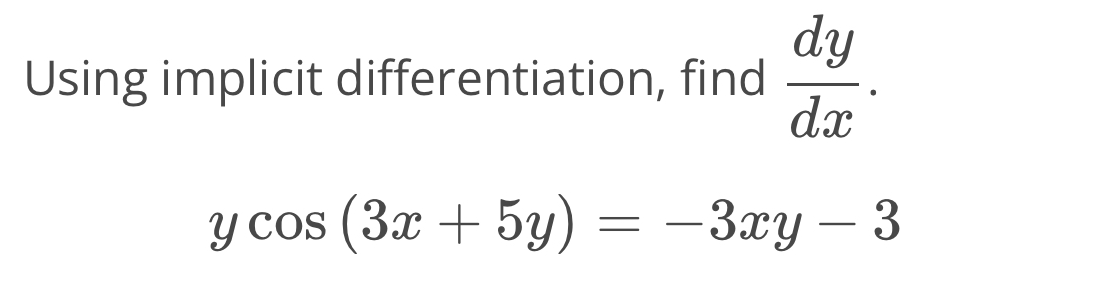Using implicit differentiation, find (dy)/(dx). y cos(3x+5y)=-3xy-3

Question

Using implicit differentiation, find  (dy)/(dx).  y cos(3x+5y)=-3xy-3

Bytelearn · Accepted Answer

Given Equation: We are given the equation y cos(3x+5y)=-3xy-3 and we need to find the derivative of y with respect to x using implicit differentiation.Implicit Differentiation: Differentiate both sides of the equation with respect to x. Remember to use the product rule for y cos(3x+5y) and the chain rule for cos(3x+5y) since y is a function of x.Left Side Differentiation: Differentiating the left side y cos(3x+5y) with respect to x gives us: y' cos(3x+5y) - y sin(3x+5y) (3 + 5y'), where y' denotes dy/dx.Right Side Differentiation: Differentiating the right side -3xy-3 with respect to x gives us: -3y - 3xy'.Combine Equations: Now we have the equation: y' cos(3x+5y) - y sin(3x+5y) (3 + 5y') = -3y - 3xy'.Isolate y': We need to solve for y'. To do this, we'll collect all terms involving y' on one side of the equation and the rest on the other side.Rearrange Terms: Rearrange the terms to isolate y': y' cos(3x+5y) + y sin(3x+5y) * 5y' - 3xy' = -3y - y sin(3x+5y) * 3.Factor Out y': Factor out y' from the left side of the equation: y' (cos(3x+5y) + 5y sin(3x+5y) - 3x) = -3y - 3y sin(3x+5y).Divide to Solve for y': Divide both sides by (cos(3x+5y) + 5y sin(3x+5y) - 3x) to solve for y': y' = (-3y - 3y sin(3x+5y)) / (cos(3x+5y) + 5y sin(3x+5y) - 3x).Final Derivative: Now we have the derivative of y with respect to x: (dy)/(dx) = y' = (-3y - 3y sin(3x+5y)) / (cos(3x+5y) + 5y sin(3x+5y) - 3x).

Using implicit differentiation, find $\frac{d y}{d x}$ . $\newline$ $y \cos (3 x+5 y)=-3 x y-3$

Full solution

More problems from Find limits involving trigonometric functions

Related topics

Using implicit differentiation, find dydx \frac{d y}{d x} dxdy​.\newlineycos⁡(3x+5y)=−3xy−3 y \cos (3 x+5 y)=-3 x y-3 ycos(3x+5y)=−3xy−3

Using implicit differentiation, find $\frac{d y}{d x}$ . $\newline$ $y \cos (3 x+5 y)=-3 x y-3$