Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

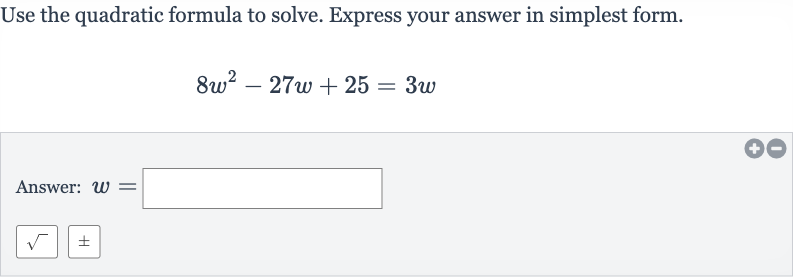
Use the quadratic formula to solve. Express your answer in simplest form. 8w^(2)-27 w+25=3w Answer: w=

Use the quadratic formula to solve. Express your answer in simplest form.\newline8w2−27w+25=3w 8 w^{2}-27 w+25=3 w \newlineAnswer: w= w=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Composition of linear and quadratic functions: find an equationright chevron icon

Full solution

Q. Use the quadratic formula to solve. Express your answer in simplest form.\newline8w2−27w+25=3w 8 w^{2}-27 w+25=3 w \newlineAnswer: w= w=
  1. Bring to Standard Form: First, we need to bring the equation to standard quadratic form, which is ax2+bx+c=0ax^2 + bx + c = 0. \newline8w2−27w+25=3w8w^2 - 27w + 25 = 3w\newlineSubtract 3w3w from both sides to get:\newline8w2−27w+25−3w=08w^2 - 27w + 25 - 3w = 0\newline8w2−30w+25=08w^2 - 30w + 25 = 0
  2. Apply Quadratic Formula: Now that we have the quadratic equation in standard form, we can apply the quadratic formula to find the solutions for ww. The quadratic formula is given by:\newlinew=−b±b2−4ac2aw = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\newlinewhere a=8a = 8, b=−30b = -30, and c=25c = 25.
  3. Calculate Discriminant: Next, we calculate the discriminant, which is the part under the square root in the quadratic formula: b2−4acb^2 - 4ac.\newlineDiscriminant = (−30)2−4(8)(25)(-30)^2 - 4(8)(25)\newlineDiscriminant = 900−800900 - 800\newlineDiscriminant = 100100
  4. Find Solutions: Since the discriminant is positive, we will have two real solutions. Now we can plug the values of aa, bb, and cc into the quadratic formula to find the solutions for ww. \newlinew=−(−30)±1002×8w = \frac{-(-30) \pm \sqrt{100}}{2 \times 8}\newlinew=30±1016w = \frac{30 \pm 10}{16}
  5. Solve for w: We will now solve for ww using the two possible values for the ±\pm sign.\newlineFirst solution:\newlinew=30+1016w = \frac{30 + 10}{16}\newlinew=4016w = \frac{40}{16}\newlinew=2.5w = 2.5\newlineSecond solution:\newlinew=30−1016w = \frac{30 - 10}{16}\newlinew=2016w = \frac{20}{16}\newlinew=1.25w = 1.25

More problems from Composition of linear and quadratic functions: find an equation

Question
Find the inverse of the function. y=x+3 y = x + 3 Write your answer in the form ax+b ax + b . Simplify any fractions. y= y = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
Find (r∘s)(x)(r \circ s)(x).\newliner(x) = 33x\newlines(x) = 22x + 55\newlineWrite your answer as a polynomial in simplest form.\newline(r∘s)(x)=(r \circ s)(x) = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
What is (f+g)(x)(f + g)(x)?\newlinef(x)=−3xf(x) = -3x\newlineg(x)=3x+1g(x) = 3x + 1\newline\newlineWrite your answer as a polynomial or a rational function in simplest form.\newline‾\underline{\hspace{3cm}}\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
What is (f∗g)(x)(f * g)(x)?\newlinef(x)=−x+4f(x) = -x + 4\newlineg(x)=4xg(x) = 4x\newline\newlineWrite your answer as a polynomial or a rational function in simplest form.\newline‾\underline{\hspace{3em}}\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the domain of (fg)(x)\left(\frac{f}{g}\right)(x)?\newlinef(x)=2xf(x) = 2x\newlineg(x)=−5x+3g(x) = -5x + 3\newlineChoices:\newline[A]All real numbers[\text{A]All real numbers}\newline[B]All real numbers except 35[\text{B]All real numbers except } \frac{3}{5}\newline[C]All real numbers except −35[\text{C]All real numbers except } -\frac{3}{5}\newline[D]All real numbers except 53[\text{D]All real numbers except } \frac{5}{3}
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the inverse of the function.\newliney = −3x-3x \newlineWrite your answer in the form ax+bax + b. Simplify any fractions.\newliney = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find (f∘g)(0)(f \circ g)(0).\newlinef(x)=6xf(x) = 6x\newlineg(x)=x2+4xg(x) = x^2 + 4x\newline(f∘g)(0)=(f \circ g)(0) = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find (f∘g)(x)(f \circ g)(x).\newlinef(x)=x2+5f(x) = x^2 + 5\newlineg(x)=4xg(x) = 4x\newlineWrite your answer as a polynomial in simplest form.\newline(f∘g)(x)=(f \circ g)(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Is f(x) f(x) the inverse function of g(x) g(x) ?\newlinef(x)=x f(x) = x \newlineg(x)=−4x g(x) = -4x \newlineChoices:\newline[yes] \text{[yes]} \newline[no] \text{[no]}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is (f∗g)(x)(f * g)(x)? f(x)=3x2+9xf(x) = 3x^2 + 9x g(x)=3xg(x) = 3x Write your answer as a polynomial or a rational function in simplest form. ______
Get tutor helpright-arrow

Posted 3 months ago

View all (132)