Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Use Pascal's Triangle to expand
(3z-4)^(4). Express your answer in simplest form.
Answer:

Use Pascal's Triangle to expand $(3 z-4)^{4}$ . Express your answer in simplest form. $\newline$ Answer:

View step-by-step help

View step-by-step help

Pascal's triangle and the Binomial Theorem

Full solution

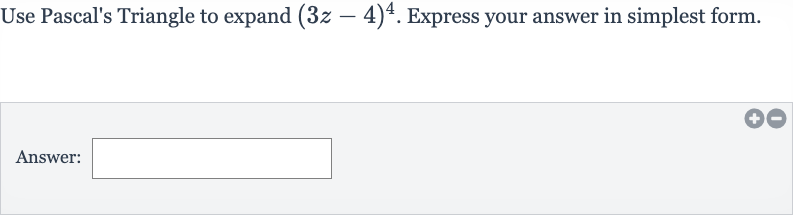
Q. Use Pascal's Triangle to expand

(3 z-4)^{4}

. Express your answer in simplest form.

\newline

Answer:

Identify Row: Identify the row of Pascal's Triangle that corresponds to the exponent $4$ . The row for the exponent $4$ in Pascal's Triangle is the fifth row (starting with row $0$ for the exponent $0$ ), which is $1, 4, 6, 4, 1$ .
Write Expansion Terms: Write out the terms of the expansion using the coefficients from Pascal's Triangle. $\newline$ The expansion will have the form: $(a+b)^4 = 1\cdot a^4\cdot b^0 + 4\cdot a^3\cdot b^1 + 6\cdot a^2\cdot b^2 + 4\cdot a^1\cdot b^3 + 1\cdot a^0\cdot b^4$ . $\newline$ In our case, $a = 3z$ and $b = -4$ .
Substitute and Simplify: Substitute $a = 3z$ and $b = -4$ into the expansion and simplify each term. $\newline$ The expansion becomes: $1\cdot(3z)^4\cdot(-4)^0 + 4\cdot(3z)^3\cdot(-4)^1 + 6\cdot(3z)^2\cdot(-4)^2 + 4\cdot(3z)^1\cdot(-4)^3 + 1\cdot(3z)^0\cdot(-4)^4$ .
Calculate Each Term: Calculate each term separately. $\newline$ $1$ st term: $1*(3z)^4*(-4)^0 = 1*81z^4*1 = 81z^4$ $\newline$ $2$ nd term: $4*(3z)^3*(-4)^1 = 4*27z^3*(-4) = -432z^3$ $\newline$ $3$ rd term: $6*(3z)^2*(-4)^2 = 6*9z^2*16 = 864z^2$ $\newline$ $4$ th term: $4*(3z)^1*(-4)^3 = 4*3z*(-64) = -768z$ $\newline$ $5$ th term: $1*(3z)^0*(-4)^4 = 1*1*256 = 256$
Combine for Final Form: Combine all the terms to get the final expanded form. $\newline$ The expanded form is: $81z^4 - 432z^3 + 864z^2 - 768z + 256$ .

More problems from Pascal's triangle and the Binomial Theorem

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 2 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 1 month ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 2 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 2 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 2 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 2 months ago