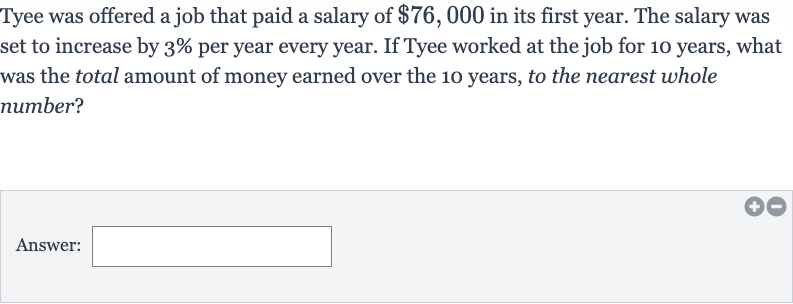
Tyee was offered a job that paid a salary of $76,000 in its first year. The salary was set to increase by 3% per year every year. If Tyee worked at the job for 10 years, what was the total amount of money earned over the 10 years, to the nearest whole number? Answer:

Question

Tyee was offered a job that paid a salary of  $76,000 in its first year. The salary was set to increase by  3% per year every year. If Tyee worked at the job for 10 years, what was the total amount of money earned over the 10 years, to the nearest whole number? Answer:

Bytelearn · Accepted Answer

Identify Salary and Rate: Identify the initial salary and the annual increase rate. Tyee's initial salary is $76,000, and it increases by 3% each year.Calculate Yearly Salaries: Calculate the salary for each year using the formula for compound interest, which is applicable here since the salary increases by a fixed percentage each year. The formula for the salary in the nth year is: Salary_n = Initial Salary * (1 + rate)^n where rate is the annual increase rate (3% or 0.03) and n is the year number.Calculate Total Over 10 Years: Calculate the total salary over 10 years by summing up the salaries for each year. Let's denote the total salary by S_total. S_total = Salary_1 + Salary_2 + ... + Salary_10 We will calculate each year's salary and add them up.Calculate Yearly Salaries: Calculate the salary for each year and keep a running total. Year 1: Salary_1 = $76,000 * (1 + 0.03)^1 = $76,000 * 1.03 = $78,280 Year 2: Salary_2 = $76,000 * (1 + 0.03)^2 = $76,000 * 1.0609 ≈ $80,628.40 Year 3: Salary_3 = $76,000 * (1 + 0.03)^3 = $76,000 * 1.092727 ≈ $83,047.25 Year 4: Salary_4 = $76,000 * (1 + 0.03)^4 = $76,000 * 1.12550881 ≈ $85,538.67 Year 5: Salary_5 = $76,000 * (1 + 0.03)^5 = $76,000 * 1.15927407 ≈ $88,104.69 Year 6: Salary_6 = $76,000 * (1 + 0.03)^6 = $76,000 * 1.19384229 ≈ $90,747.41 Year 7: Salary_7 = $76,000 * (1 + 0.03)^7 = $76,000 * 1.22933716 ≈ $93,469.02 Year 8: Salary_8 = $76,000 * (1 + 0.03)^8 = $76,000 * 1.26577698 ≈ $96,272.71 Year 9: Salary_9 = $76,000 * (1 + 0.03)^9 = $76,000 * 1.30317029 ≈ $99,161.66 Year 10: Salary_10 = $76,000 * (1 + 0.03)^10 = $76,000 * 1.34391626 ≈ $102,138.16  Now, add all the yearly salaries to get the total: S_total = $78,280 + $80,628.40 + $83,047.25 + $85,538.67 + $88,104.69 + $90,747.41 + $93,469.02 + $96,272.71 + $99,161.66 + $102,138.16Find Total Salary: Perform the addition to find the total salary over 10 years. S_total ≈ $78,280 + $80,628.40 + $83,047.25 + $85,538.67 + $88,104.69 + $90,747.41 + $93,469.02 + $96,272.71 + $99,161.66 + $102,138.16 S_total ≈ $897,388.97Round Total Salary: Round the total salary to the nearest whole number as requested. S_total ≈ $897,389

Tyee was offered a job that paid a salary of $\$ 76,000$ in its first year. The salary was set to increase by $3 \%$ per year every year. If Tyee worked at the job for $10$ years, what was the total amount of money earned over the $10$ years, to the nearest whole number? $\newline$ Answer:

Full solution

More problems from Exponential growth and decay: word problems

Related topics