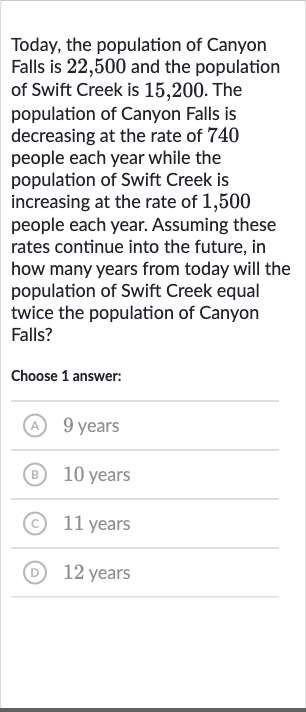
Today, the population of Canyon Falls is $22$ , $500$ and the population of Swift Creek is $15$ , $200$ . The population of Canyon Falls is decreasing at the rate of $740$ people each year while the population of Swift Creek is increasing at the rate of $1$ , $500$ people each year. Assuming these rates continue into the future, in how many years from today will the population of Swift Creek equal twice the population of Canyon Falls? $\newline$ Choose $1$ answer: $\newline$ (A) $9$ years $\newline$ (B) $\mathbf{1 0}$ years $\newline$ (C) $\mathbf{1 1}$ years $\newline$ (D) $12$ years

View step-by-step help

Home

Math Problems

Grade 8

Solve equations with variables on both sides: word problems

Full solution

Q. Today, the population of Canyon Falls is

22

500

and the population of Swift Creek is

15

200

. The population of Canyon Falls is decreasing at the rate of

740

people each year while the population of Swift Creek is increasing at the rate of

1

500

people each year. Assuming these rates continue into the future, in how many years from today will the population of Swift Creek equal twice the population of Canyon Falls?

\newline

Choose

1

answer:

\newline

(A)

9

years

\newline

(B)

\mathbf{1 0}

years

\newline

(C)

\mathbf{1 1}

years

\newline

(D)

12

years

Set Up Equation: Let's denote the number of years from today as $y$ . We need to set up an equation that represents the situation where the population of Swift Creek equals twice the population of Canyon Falls after $y$ years. $\newline$ Canyon Falls population after $y$ years: $22,500 - 740y$ $\newline$ Swift Creek population after $y$ years: $15,200 + 1,500y$ $\newline$ The equation we need to solve is: $\newline$ $15,200 + 1,500y = 2(22,500 - 740y)$
Distribute $2$ : Now, let's distribute the $2$ on the right side of the equation: $\newline$ $15,200 + 1,500y = 45,000 - 1,480y$
Combine Like Terms: Next, we combine like terms by adding $1,480y$ to both sides of the equation and subtracting $15,200$ from both sides: $\newline$ $15,200 + 1,500y + 1,480y = 45,000 - 1,480y + 1,480y$ $\newline$ $15,200 - 15,200 + 2,980y = 45,000 - 15,200$ $\newline$ $2,980y = 29,800$
Solve for y: Now, we solve for ＂y＂ by dividing both sides of the equation by $2,980$ : $\newline$ $y = \frac{29,800}{2,980}$
Perform Division: Performing the division gives us the number of years: $y = 10$