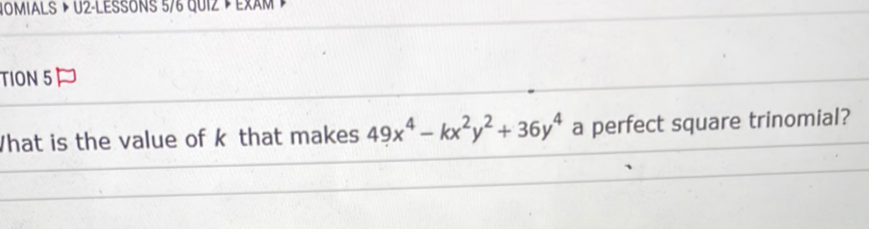Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the value of k that makes 49x^(4)-kx^(2)y^(2)+36y^(4) a perfect square trinomial?

What is the value of k k that makes 49x4−kx2y2+36y4 49 x^{4}-k x^{2} y^{2}+36 y^{4} a perfect square trinomial?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Complete the squareright chevron icon

Full solution

Q. What is the value of k k that makes 49x4−kx2y2+36y4 49 x^{4}-k x^{2} y^{2}+36 y^{4} a perfect square trinomial?
  1. Identify Perfect Square Trinomial: To make 49x4−kx2y2+36y449x^{4}-kx^{2}y^{2}+36y^{4} a perfect square trinomial, the middle term coefficient kk must be such that the trinomial can be factored into (ax2+by2)2.(ax^{2} + by^{2})^{2}.
  2. Recognize Perfect Squares: The first term 49x449x^{4} is a perfect square, (7x2)2(7x^2)^2, and the last term 36y436y^{4} is a perfect square, (6y2)2(6y^2)^2.
  3. Calculate Middle Term Coefficient: For the trinomial to be a perfect square, the middle term coefficient kk must be 22 times the product of the square roots of the first and last terms, so k=2×7x2×6y2k = 2 \times 7x^2 \times 6y^2.
  4. Determine k Value: Calculate k: k=2×7×6×x2×y2k = 2 \times 7 \times 6 \times x^2 \times y^2.
  5. Determine k Value: Calculate k: k=2×7×6×x2×y2k = 2 \times 7 \times 6 \times x^2 \times y^2.k=84x2y2k = 84x^2y^2.

More problems from Complete the square

Question
Solve for v v .\newlinev2+8v+12=0 v^2+8v+12=0\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlinev= v=_____
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve for u u .\newlineu2=9 u^2 = 9 \newlineWrite your answers as integers or as proper or improper fractions in simplest form.\newlineu= u = _____ or u= u = _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinek2−20k+_____k^2 - 20k + \_\_\_\_\_
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve by completing the square.\newlineu2−24u−23=0u^2 - 24u - 23 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`u` = ________ or `u` =______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the discriminant. \newline2q2−9q+8=02q^2 - 9q + 8 = 0\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve the system of equations.\newliney=22x−38 y = 22x - 38 \newliney=x2+11x−14 y = x^2 + 11x - 14 \newlineWrite the coordinates in exact form. Simplify all fractions and radicals.\newline(_,_) (\_,\_) \newline(_,_) (\_,\_)
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve for aa.\newline(a+5)(a+1)=0(a + 5)(a + 1) = 0\newlineWrite your answers as integers or as proper or improper fractions in simplest form.\newlinea=a = _____ or a=a = _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Let p=x2−7 p=x^{2}-7 . Which equation is equivalent to (x2−7)2−4x2+28=5 (x^{2}-7)^{2}-4x^{2}+28=5 in terms of p p ? Choose 11 answer: \newline(A) p2−4p+23=0 p^{2}-4p+23=0 \newline(B) p2+4p−5=0 p^{2}+4p-5=0 \newline(C) p2−4p−5=0 p^{2}-4p-5=0 \newline(D) p2+4p+23=0 p^{2}+4p+23=0
Get tutor helpright-arrow

Posted 2 months ago

Question
Let m=2x+3m=2x+3. Which equation is equivalent to (2x+3)2−14x−21=−6(2x+3)^{2}-14x-21=-6 in terms of mm? Choose 11 answer: \newline(A) m2+7m+6=0m^{2}+7m+6=0 \newline(B) m2−7m−15=0m^{2}-7m-15=0 \newline(C) m2−7m+6=0m^{2}-7m+6=0 \newline(D) m2+7m−15=0m^{2}+7m-15=0
Get tutor helpright-arrow

Posted 2 months ago

Question
Let m=x2+3m=x^{2}+3. Which equation is equivalent to (x2+3)2+7x2+21=−10(x^{2}+3)^{2}+7x^{2}+21=-10 in terms of mm? Choose 11 answer:\newline(A) m2−7m+31=0m^{2}-7m+31=0\newline(B) m2+7m+31=0m^{2}+7m+31=0\newline(C) m2−7m+10=0m^{2}-7m+10=0\newline(D) m2+7m+10=0m^{2}+7m+10=0
Get tutor helpright-arrow

Posted 2 months ago

View all (40)