AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
The second derivative of the function is defined by for \( -0.5
Full solution
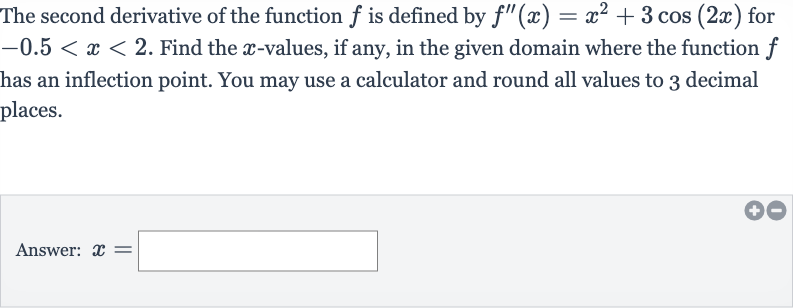
Q. The second derivative of the function is defined by for . Find the -values, if any, in the given domain where the function has an inflection point. You may use a calculator and round all values to decimal places.Answer:
- Set up critical points equation: To find the inflection points of the function , we need to determine where the second derivative changes sign. This occurs when . Let's set up the equation to find the critical points:
- Solve for : Now we need to solve the equation for . This is a transcendental equation, and we will use a calculator to find the solutions within the given domain -0.5 < x < 2. We are looking for the -values where the second derivative equals zero.
- Graph function : Using a calculator, we can graph the function and look for the x-intercepts within the domain -0.5 < x < 2. The x-intercepts will be the x-values where .
- Identify potential inflection points: After graphing the function, we find that the x-intercepts (rounded to three decimal places) within the domain are approximately , , and . These are the potential inflection points.
- Confirm inflection points: To confirm that these -values are indeed inflection points, we need to check the sign change of around each of these values. If the sign of changes from positive to negative or from negative to positive as we pass through these -values, then they are inflection points.
- Confirm inflection points: To confirm that these -values are indeed inflection points, we need to check the sign change of around each of these values. If the sign of changes from positive to negative or from negative to positive as we pass through these -values, then they are inflection points.By testing values just to the left and right of , , and , we can confirm that the sign of changes at each of these points, indicating that they are indeed inflection points.
