Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

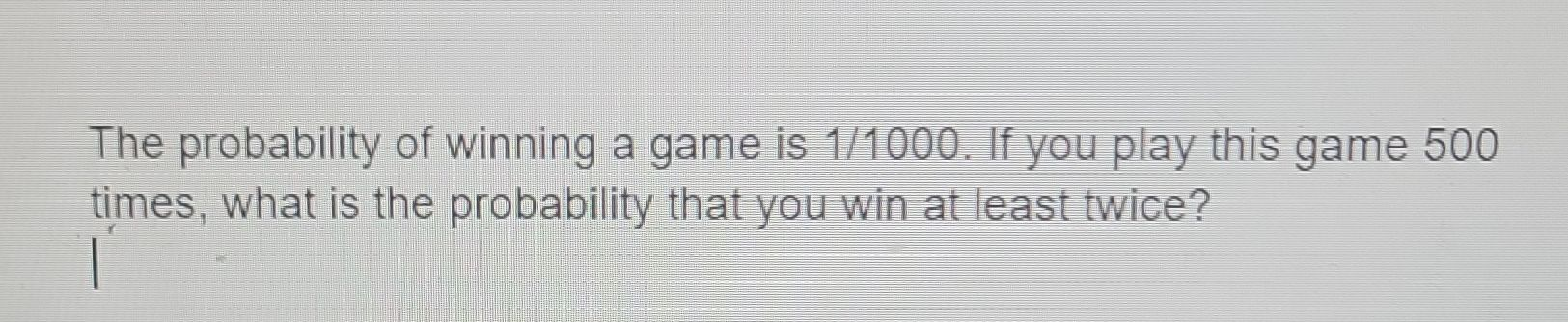
The probability of winning a game is
1//1000. If you play this game 500 times, what is the probability that you win at least twice?

The probability of winning a game is $1 / 1000$ . If you play this game $500$ times, what is the probability that you win at least twice?

View step-by-step help

View step-by-step help

Probability of independent and dependent events

Full solution

Q. The probability of winning a game is

1 / 1000

. If you play this game

500

times, what is the probability that you win at least twice?

Identify probability of not winning: Identify the probability of not winning the game. $\newline$ The probability of not winning the game is the complement of the probability of winning the game. $\newline$ Probability of not winning = $1 - \text{Probability of winning} = 1 - \frac{1}{1000} = \frac{999}{1000}$ .
Calculate probability of winning once: Calculate the probability of winning exactly once in $500$ tries. $\newline$ This can be done using the binomial probability formula: $\newline$ $P(X = k) = C(n, k) \cdot (p^k) \cdot ((1-p)^{(n-k)})$ $\newline$ Where: $\newline$ $P(X = k)$ is the probability of $k$ successes in $n$ trials, $\newline$ $C(n, k)$ is the number of combinations of $n$ things taken $k$ at a time, $\newline$ $p$ is the probability of success on a single trial, and $\newline$ $n$ is the number of trials. $\newline$ For winning exactly once: $\newline$ $P(X = k) = C(n, k) \cdot (p^k) \cdot ((1-p)^{(n-k)})$ $0$ $\newline$ $P(X = k) = C(n, k) \cdot (p^k) \cdot ((1-p)^{(n-k)})$ $1$
Calculate probability of never winning: Calculate the probability of never winning in $500$ tries. $\newline$ This is simply the probability of not winning raised to the power of the number of tries: $\newline$ $P(X = 0) = (\frac{999}{1000})^{500}$
Calculate probability of winning at least twice: Calculate the probability of winning at least twice. The probability of winning at least twice is the complement of the probability of winning fewer than two times (which includes winning exactly once and never winning). P(X \geq 2) = 1 - P(X < 2) P(X < 2) = P(X = 0) + P(X = 1) $P(X \geq 2) = 1 - (P(X = 0) + P(X = 1))$
Perform calculations: Perform the calculations using the results from Steps $2$ and $3$ . $\newline$ $P(X \geq 2) = 1 - ((999/1000)^{500} + 500 \times (1/1000) \times (999/1000)^{499})$
Simplify expression: Simplify the expression. This step involves arithmetic calculations to simplify the expression obtained in Step $5$ .

More problems from Probability of independent and dependent events

Question

6

-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage.

\newline

Posted 5 months ago

Question

9

college students running for student government class president. The candidates include

7

education majors.

\newline

6

of the candidates are randomly chosen to give the first

6

speeches, what is the probability that all of them are education majors?

\newline

Write your answer as a decimal rounded to four decimal places.

Posted 8 months ago

Question

In an experiment, the probability that event

A

\frac{2}{7}

, the probability that event

B

\frac{7}{9}

, and the probability that events

A

B

\frac{1}{9}

\newline

A

B

independent events?

\newline

\newline

\text{yes}

\newline

\text{no}

Posted 8 months ago

Question

At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.

\newline

The probability that a competitor reacted in over

0.7

0.6

, the probability that a competitor was female is

0.4

, and the probability that a competitor reacted in over

0.7

seconds and was female is

0.3

\newline

What is the probability that a randomly chosen competitor reacted in over

0.7

seconds or was female?

\newline

Write your answer as a whole number, decimal, or simplified fraction.

\newline

Posted 8 months ago

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 7 months ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 8 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 8 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 8 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 8 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant