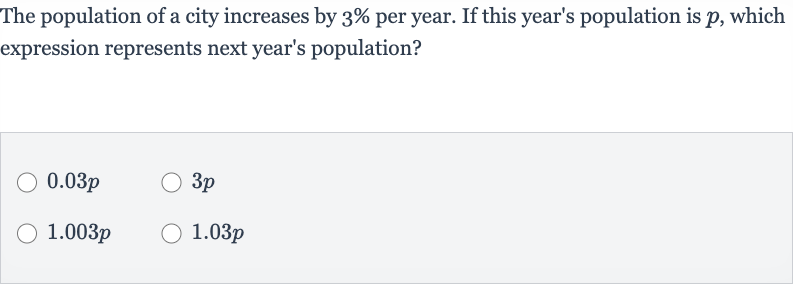AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
The population of a city increases by per year. If this year's population is , which expression represents next year's population?
Full solution
Q. The population of a city increases by per year. If this year's population is , which expression represents next year's population?
- Understand the problem: Understand the problem.We need to find the expression that represents the population of a city next year, given that the population this year is and it increases by annually.
- Translate percentage increase: Translate the percentage increase into a decimal.A increase can be represented as in decimal form.
- Apply increase to current population: Apply the percentage increase to this year's population.To find next year's population, we add the increase to the current population. This is equivalent to multiplying the current population by plus the percentage increase in decimal form.
- Write expression for next year's population: Write the expression for next year's population.Next year's population is this year's population plus % of this year's population. In mathematical terms, this is .
- Simplify the expression: Simplify the expression.Combine like terms by factoring out from the expression.$p + (\(0\).\(03\) \times p) = p \times (\(1\) + \(0\).\(03\)) = p \times \(1\).\(03\)
- Identify correct expression: Identify the correct expression from the given options.\(\newline\)The expression that represents next year's population is \(p \times 1.03\).
