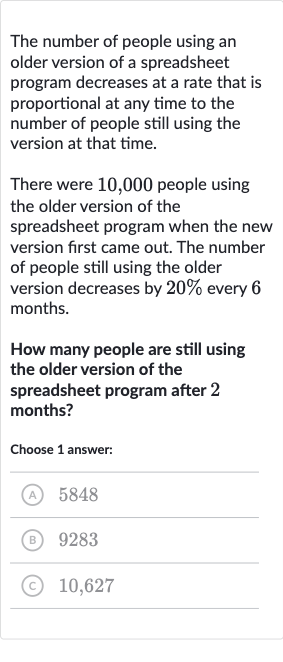
The number of people using an older version of a spreadsheet program decreases at a rate that is proportional at any time to the number of people still using the version at that time. There were 10,000 people using the older version of the spreadsheet program when the new version first came out. The number of people still using the older version decreases by 20% every 6 months. How many people are still using the older version of the spreadsheet program after 2 months? Choose 1 answer: (A) 5848 (B) 9283 (C) 10,627

Question

The number of people using an older version of a spreadsheet program decreases at a rate that is proportional at any time to the number of people still using the version at that time. There were 10,000 people using the older version of the spreadsheet program when the new version first came out. The number of people still using the older version decreases by  20% every 6 months. How many people are still using the older version of the spreadsheet program after 2 months? Choose 1 answer: (A) 5848 (B) 9283 (C) 10,627

Bytelearn · Accepted Answer

Understand and Determine Formula: Understand the problem and determine the formula to use. The problem states that the number of people using an older version of a spreadsheet program decreases by 20% every 6 months. This is an exponential decay problem, and we can use the formula for exponential decay, which is N(t) = N_0 * e^(-kt), where N(t) is the number of users at time t, N_0 is the initial number of users, k is the decay constant, and t is the time in the same units as the rate of decay.Calculate Decay Constant: Calculate the decay constant k. Since the number of users decreases by 20% every 6 months, we can find the decay constant k by using the half-life formula, which is N(t) = N_0 * (1/2)^(t/half-life). Here, the half-life is not exactly applicable since it's not a 50% decrease, but we can adjust the formula to fit a 20% decrease: N(t) = N_0 * (0.8)^(t/6), where t is in months.Calculate Users After 2 Months: Calculate the number of users after 2 months. We need to plug in the values into the adjusted formula from Step 2. Let's denote the number of users after 2 months as N(2). We have N_0 = 10,000 and t = 2 months. So, N(2) = 10,000 * (0.8)^(2/6).Perform Calculation: Perform the calculation. Now we calculate N(2) = 10,000 * (0.8)^(2/6). First, we calculate the exponent: (2/6) = 1/3. Then we calculate 0.8^(1/3).Find Value of 0.8^1/3: Find the value of 0.8 raised to the power of 1/3. Calculating 0.8^(1/3) can be done using a calculator or estimating the cube root of 0.8. However, this is where I realize there is a mistake in the approach. The decay rate is given for a 6-month period, not monthly, so we cannot directly apply the 20% decrease to a 2-month period using the formula in this way. We need to find the monthly decay rate first and then apply it to the 2-month period. This is a math error.

Full solution

More problems from Write an equation word problem

Related topics