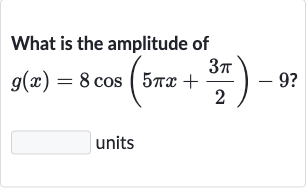Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the amplitude of g(x)=8cos(5pi x+(3pi)/(2))-9? units

What is the amplitude of\newlineg(x)=8cos⁡(5πx+3π2)−9? g(x)=8 \cos \left(5 \pi x+\frac{3 \pi}{2}\right)-9 ? \newlineunits

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 8right chevron icon
Solve multi-step equations with fractional coefficientsright chevron icon

Full solution

Q. What is the amplitude of\newlineg(x)=8cos⁡(5πx+3π2)−9? g(x)=8 \cos \left(5 \pi x+\frac{3 \pi}{2}\right)-9 ? \newlineunits
  1. Amplitude of cosine function: The amplitude of a cosine function is the coefficient of the cosine term, which is the absolute value of the number that multiplies the cosine function. In the given function g(x)=8cos⁡(5πx+3π2)−9g(x) = 8\cos(5\pi x + \frac{3\pi}{2}) - 9, the coefficient of the cosine term is 88.
  2. Finding the amplitude: To find the amplitude, we do not need to consider the horizontal shift, vertical shift, or the period of the function. The amplitude is simply the absolute value of the coefficient of the cosine term, which is already positive in this case. Therefore, the amplitude of g(x)g(x) is 88.

More problems from Solve multi-step equations with fractional coefficients

Question
What happens to the value of the expression 80−2r 80-2 r as r r decreases?\newlineChoose 11 answer:\newline(A) It increases.\newline(B) It decreases.\newline(C) It stays the same.
Get tutor helpright-arrow

Posted 8 months ago

Question
Solve for q q .\newline3(q+43)=2 3\left(q+\frac{4}{3}\right)=2
Get tutor helpright-arrow

Posted 7 months ago

Question
Solve for f f .\newline0.3=0.5f−0.7 0.3=0.5 f-0.7
Get tutor helpright-arrow

Posted 7 months ago

Question
Solve for a a .\newline0.25a+0.5=4.5 0.25 a+0.5=4.5
Get tutor helpright-arrow

Posted 7 months ago

Question
Solve for d d .\newline32=5d−12 \frac{3}{2}=5 d-\frac{1}{2}
Get tutor helpright-arrow

Posted 7 months ago

Question
Consider the expression 13bwh \frac{1}{3} b w h .\newlineComplete 22 descriptions of the parts of the expression.\newline11. The entire expression is the product of □\square.\newline22. In this context, 13 \frac{1}{3} is a □\square.
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the sign of −8813+8813? -\frac{88}{13}+\frac{88}{13} ? \newlineChoose 11 answer:\newline(A) Positive\newline(B) Negative\newline(C) Neither positive nor negative-the sum is zero.
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the sign of 3.456+(−3.456)? 3.456+(-3.456) ? \newlineChoose 11 answer:\newline(A) Positive\newline(B) Negative\newline(C) Neither positive nor negative-the sum is zero.
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the sign of 123123+(−123123) 123 \frac{1}{23}+\left(-123 \frac{1}{23}\right) ?\newlineChoose 11 answer:\newline(A) Positive\newline(B) Negative\newline(C) Neither positive nor negative-the sum is zero.
Get tutor helpright-arrow

Posted 7 months ago

Question
late scale drawing...\newlineCopy of Cakes to Sn.\newlineCen We Prevent Sch\newlineColinge Bouts\newlinee? Resend it,\newlineKhan Academy\newlineDonate ए\newlineemmy h\newlinelazing!\newlineweek\newlinestreak\newlineLevel 1414\newlineGoogle Classroom\newlineMicrosoft Teams\newlinePolygon F F has an area of 3636 square units. Aimar drew a scaled version of Polygon F F and labeled it Polygon G G . Polygon G G has an area of 44 square units.\newlineWhat scale factor did Aimar use to go from Polygon F F to Polygon G G ? □ \square
Get tutor helpright-arrow

Posted 3 hours ago

View all (19)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant