Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The length of a rectangle's diagonal is
2sqrt29, and the length of the longer side is 10 . What is the area of the rectangle?
A) 116
B)
20sqrt29
C)
10sqrt29
D) 40

The length of a rectangle's diagonal is $2 \sqrt{29}$ , and the length of the longer side is $10$ . What is the area of the rectangle? $\newline$ A) $116$ $\newline$ B) $20 \sqrt{29}$ $\newline$ C) $10 \sqrt{29}$ $\newline$ D) $40$

View step-by-step help

View step-by-step help

Transformations of functions

Full solution

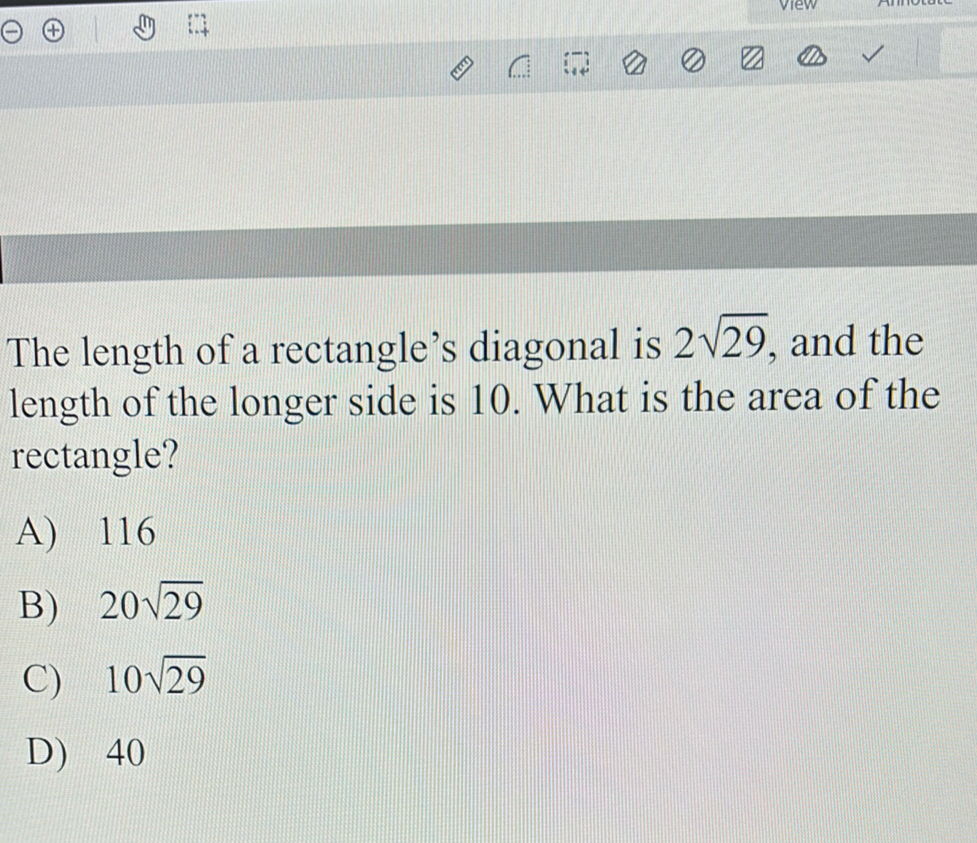
Q. The length of a rectangle's diagonal is

2 \sqrt{29}

, and the length of the longer side is

10

. What is the area of the rectangle?

\newline

A)

116

\newline

B)

20 \sqrt{29}

\newline

C)

10 \sqrt{29}

\newline

D)

40

Identify Rectangle Dimensions: To find the area of the rectangle, we need to know both the length and the width. We already know the length is $10$ . We can use the Pythagorean theorem to find the width, since the diagonal ( $d$ ), length ( $l$ ), and width ( $w$ ) of a rectangle form a right triangle: $d^2 = l^2 + w^2$ .
Calculate Diagonal Squared: We are given that the diagonal $d$ is $2\sqrt{29}$ . Let's square this to find $d^2$ : $(2\sqrt{29})^2 = 4 \times 29 = 116$ .
Calculate Length Squared: We know the length $l$ is $10$ , so let's square this to find $l^2$ : $10^2 = 100$ .
Substitute into Pythagorean Theorem: Now we can substitute $d^2$ and $l^2$ into the Pythagorean theorem to find $w^2$ : $116 = 100 + w^2$ .
Solve for Width: Subtract $100$ from both sides to solve for $w^2$ : $116 - 100 = w^2$ , so $w^2 = 16$ .
Find Width: Take the square root of both sides to find $w$ : $\sqrt{w^2} = \sqrt{16}$ , so $w = 4$ .
Calculate Area: Now that we have both the length ( $10$ ) and the width ( $4$ ), we can find the area of the rectangle by multiplying the length by the width: $\text{Area} = \text{length} \times \text{width} = 10 \times 4$ .
Final Area Calculation: Calculate the area: $10 \times 4 = 40$ .

More problems from Transformations of functions

Question

g(x)

g(x)

is the reflection across the x-axis of

f(x)=9|x+2|-4

\newline

\newline

\text{}(A)g(x) = 9|x+2| - 4\text{]}

\newline

\text{}(B)g(x) = 9|x-2| - 4\text{]}

\newline

\text{}(C)g(x)=-9|x-2| +4\text{]}

\newline

\text{(D)}g(x) = -9|x + 2| + 4\text{]}

Posted 2 months ago

Question

What does the transformation

f(x) \mapsto f(x - 4)

do to the graph of

f(x)

\newline

\newline

\text{translates it } 4 \text{ units right}

\newline

\text{translates it } 4 \text{ units down}

\newline

\text{translates it } 4 \text{ units left}

\newline

\text{translates it } 4 \text{ units up}

Posted 2 months ago

Question

What does the transformation

f(x) \mapsto f(4x)

do to the graph of

f(x)

\newline

\newline

[A] stretches it vertically

\newline

[B] stretches it horizontally

\newline

[C]shrinks it horizontally

\newline

[D]shrinks it vertically

Posted 1 month ago

Question

g(x)

g(x)

is the translation

9

f(x) = 10x + 8

\newline

\newline

g(x) = 10x - 82

\newline

g(x) = 10x + 98

\newline

g(x) = 10x - 1

\newline

g(x) = 10x + 17

Posted 2 months ago

Question

What kind of transformation converts the graph of

f(x) = -3x^2 - 4

into the graph of

g(x) = -3x^2 + 6

\newline

\newline

\text{[A]translation 10 units up}

\newline

\text{[B]translation 10 units down}

\newline

\text{[C]translation 10 units left}

\newline

\text{[D]translation 10 units right}

Posted 1 month ago

Question

y=x^{2}

is scaled vertically by a factor of

7

. What is the equation of the new parabola?

\newline

y=

Posted 4 months ago

Question

y=x^{2}

is shifted down by

6

units and to the right by

5

\newline

What is the equation of the new parabola?

\newline

y=

Posted 4 months ago

Question

y=x^{2}

is shifted up by

2

units and to the right by

3

\newline

What is the equation of the new parabola?

\newline

y=

Posted 1 month ago

Question

y=x^{2}

is reflected across the

x

-axis and then scaled vertically by a factor of

5

\newline

What is the equation of the new parabola?

\newline

y=\square

Posted 2 months ago

Question

y=x^{2}

is scaled vertically by a factor of

\frac{1}{10}

\newline

What is the equation of the new parabola?

\newline

y=

Posted 3 months ago