Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

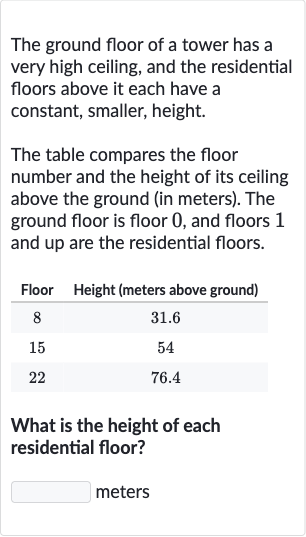
The ground floor of a tower has a very high ceiling, and the residential floors above it each have a constant, smaller, height.
The table compares the floor number and the height of its ceiling above the ground (in meters). The ground floor is floor 0 , and floors 1 and up are the residential floors.

Floor
Height (meters above ground)

8
31.6

15
54

22
76.4

What is the height of each residential floor?
meters

The ground floor of a tower has a very high ceiling, and the residential floors above it each have a constant, smaller, height. $\newline$ The table compares the floor number and the height of its ceiling above the ground (in meters). The ground floor is floor $0$ , and floors $1$ and up are the residential floors. $\newline$ \begin{tabular}{cc} $\newline$ Floor & Height (meters above ground) \\ $\newline$ \hline $8$ & $31$ . $6$ \\ $\newline$ $15$ & $54$ \\ $\newline$ $22$ & $76$ . $4$ $\newline$ \end{tabular} $\newline$ What is the height of each residential floor? $\newline$ meters

View step-by-step help

View step-by-step help

Interpret the slope and y-intercept of a linear function

Full solution

Q. The ground floor of a tower has a very high ceiling, and the residential floors above it each have a constant, smaller, height.

\newline

The table compares the floor number and the height of its ceiling above the ground (in meters). The ground floor is floor

0

, and floors

1

and up are the residential floors.

\newline

\begin{tabular}{cc}

\newline

Floor & Height (meters above ground) \\

\newline

\hline

8

&

31

.

6

\\

\newline

15

&

54

\\

\newline

22

&

76

.

4

\newline

\end{tabular}

\newline

What is the height of each residential floor?

\newline

meters

Calculate Height Difference: First, we need to find the difference in height between two known floors to determine the height of a single residential floor. We can use the data for floors $8$ and $15$ for this calculation. $\newline$ Height of floor $15$ - Height of floor $8$ = Difference in height over $7$ floors. $\newline$ $54$ meters - $31.6$ meters = $22.4$ meters over $7$ floors.
Find Height per Floor: Next, we divide the difference in height by the number of floors to find the height of one residential floor. $\newline$ $22.4$ meters $\div$ $7$ floors = Height of one residential floor. $\newline$ $3.2$ meters per floor.
Verify Calculation with Another Set of Floors: To ensure there is no math error, we can check our calculation by using the height difference between floors $15$ and $22$ . $\newline$ Height of floor $22$ - Height of floor $15$ = Difference in height over $7$ floors. $\newline$ $76.4$ meters - $54$ meters = $22.4$ meters over $7$ floors.
Confirm Height per Floor: Again, we divide the difference in height by the number of floors to confirm the height of one residential floor. $\newline$ $22.4$ meters $\div$ $7$ floors = Height of one residential floor. $\newline$ $3.2$ meters per floor.

More problems from Interpret the slope and y-intercept of a linear function

Question

Igbo uploaded a funny video of his cat onto a website.

\newline

The relationship between the elapsed time,

d

, in days, since the video was first uploaded, and the total number of views,

V(d)

, that the video received is modeled by the following function.

\newline

V(d)=10^{1.5 d}

\newline

How many days will it take for the video to receive

1,000,000

views? Round your answer, if necessary, to the nearest hundredth.

\newline

Posted 10 months ago

Question

Hannah reads at a constant rate of

3

8

\newline

Write an equation that shows the relationship between

p

, the number of pages she reads, and

m

, the number of minutes she spends reading.

\newline

Do NOT use a mixed number.

Posted 9 months ago

Question

20 l+25 g-10

gives the number of dollars that Josie makes from mowing

l

lawns and raking

g

\newline

How many dollars does Josie make from raking

4

gardens and mowing

3

\newline

Posted 9 months ago

Question

The population of a town grows at a rate of

r(t)

people per year (where

t

is time in years).

\newline

\int_{2}^{4} r(t) d t

\newline

1

\newline

(A) The change in number of people between the second and the fourth year.

\newline

(B) The time it took for the town to grow from a population of

2

people to a population of

4

\newline

(C) The number of people in the town on the fourth year.

\newline

(D) The average rate at which the population grew between the second and the fourth year.

Posted 9 months ago

Question

The cumulative profit a business has earned is changing at a rate of

r(t)

dollars per day (where

t

is the time in days). In the first

30

days, the business earned a cumulative profit of

\$ 1700

\newline

1700+\int_{30}^{90} r(t) d t

\newline

1

\newline

(A) The time it takes for the cumulative profit to increase another

\$ 1700

after the first

30

\newline

(B) The cumulative profit the business has earned as of day

90

\newline

(C) The rate at which the cumulative profit was increasing when

t=90

\newline

(D) The change in the cumulative profit between days

30

90

Posted 9 months ago

Question

A habitat of prairie dogs can support

m

\newline

The habitat's population,

p

, grows proportionally to the product of the current population and the difference between

m

p

\newline

Which equation describes this relationship?

\newline

1

\newline

\frac{d p}{d t}=k p(m-p)

\newline

\frac{d p}{d t}=\frac{k m}{m-p}

\newline

\frac{d p}{d t}=\frac{k p}{m-p}

\newline

\frac{d p}{d t}=k m(m-p)

Posted 9 months ago

Question

A young sumo wrestler decided to go on a special high-protein diet to gain weight rapidly. After

11

months, he weighed

140

kilograms. He gained weight at a rate of

5.5

kilograms per month.

\newline

y

represent the sumo wrestler's weight (in kilograms) after

x

\newline

Complete the equation for the relationship between the weight and number of months.

\newline

y=\square

Posted 9 months ago

Question

Seb bikes at a constant rate of

20

kilometers per hour.

1

. Write an equation that represents the distance, in kilometers, Seb travels

(b)

based on how many hours he bikes

(t)

2

. How far will Seb travel if he bikes at this rate for

3

\_

Posted 8 months ago

Question

Tyshawn was out at a restaurant for dinner when the bill came. He wanted to leave a tip of

28 \%

. What number should he multiply the cost of the meal by to find the total plus tip in one step?

\newline

Posted 8 months ago

Question

You pick a card at random, put it back, and then pick another card at random.

\newline

4

\newline

5

\newline

6

\newline

7

\newline

What is the probability of picking a number greater than

5

and then picking a

4

\newline

Write your answer as a percentage.

Posted 1 month ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant