Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

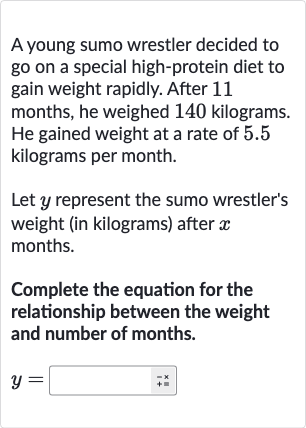
A young sumo wrestler decided to go on a special high-protein diet to gain weight rapidly. After 11 months, he weighed 140 kilograms. He gained weight at a rate of 5.5 kilograms per month.
Let
y represent the sumo wrestler's weight (in kilograms) after
x months.
Complete the equation for the relationship between the weight and number of months.

y=◻

A young sumo wrestler decided to go on a special high-protein diet to gain weight rapidly. After $11$ months, he weighed $140$ kilograms. He gained weight at a rate of $5.5$ kilograms per month. $\newline$ Let $y$ represent the sumo wrestler's weight (in kilograms) after $x$ months. $\newline$ Complete the equation for the relationship between the weight and number of months. $\newline$ $y=\square$

View step-by-step help

View step-by-step help

Write a linear function: word problems

Full solution

Q. A young sumo wrestler decided to go on a special high-protein diet to gain weight rapidly. After

11

months, he weighed

140

kilograms. He gained weight at a rate of

5.5

kilograms per month.

\newline

Let

y

represent the sumo wrestler's weight (in kilograms) after

x

months.

\newline

Complete the equation for the relationship between the weight and number of months.

\newline

y=\square

Identify initial weight: Identify the initial weight of the sumo wrestler. $\newline$ Since the sumo wrestler gained weight over $11$ months, we need to find out his initial weight before he started gaining weight. $\newline$ We know that he gained $5.5$ kilograms each month for $11$ months, which totals $5.5 \, \text{kg/month} \times 11 \, \text{months} = 60.5$ kilograms. $\newline$ To find the initial weight, we subtract the total weight gained from his weight after $11$ months. $\newline$ Initial weight $=$ Final weight $-$ Weight gained $\newline$ Initial weight $= 140 \, \text{kg} - 60.5 \, \text{kg}$
Calculate initial weight: Calculate the initial weight. $\newline$ Initial weight = $140\,\text{kg} - 60.5\,\text{kg}$ $\newline$ Initial weight = $79.5\,\text{kg}$ $\newline$ This is the weight of the sumo wrestler before he started the diet.
Write equation for weight: Write the equation for the sumo wrestler's weight after $x$ months. $\newline$ We know that the sumo wrestler gains $5.5$ kilograms each month. Therefore, the weight after $x$ months can be calculated by adding the weight gained over $x$ months to the initial weight. $\newline$ Weight after $x$ months = Initial weight + (Weight gained per month * Number of months) $\newline$ $y =$ Initial weight + $(5.5 \, \text{kg/month} \times x)$
Substitute initial weight: Substitute the initial weight into the equation. $\newline$ We have already calculated the initial weight to be $79.5\,\text{kg}$ . $\newline$ $y = 79.5\,\text{kg} + (5.5\,\text{kg}/\text{month} \times x)$ $\newline$ This is the equation that represents the sumo wrestler's weight after $x$ months.

More problems from Write a linear function: word problems

Question

Igbo uploaded a funny video of his cat onto a website.

\newline

The relationship between the elapsed time,

d

, in days, since the video was first uploaded, and the total number of views,

V(d)

, that the video received is modeled by the following function.

\newline

V(d)=10^{1.5 d}

\newline

How many days will it take for the video to receive

1,000,000

views? Round your answer, if necessary, to the nearest hundredth.

\newline

Posted 8 months ago

Question

Hannah reads at a constant rate of

3

8

\newline

Write an equation that shows the relationship between

p

, the number of pages she reads, and

m

, the number of minutes she spends reading.

\newline

Do NOT use a mixed number.

Posted 7 months ago

Question

20 l+25 g-10

gives the number of dollars that Josie makes from mowing

l

lawns and raking

g

\newline

How many dollars does Josie make from raking

4

gardens and mowing

3

\newline

Posted 7 months ago

Question

The population of a town grows at a rate of

r(t)

people per year (where

t

is time in years).

\newline

\int_{2}^{4} r(t) d t

\newline

1

\newline

(A) The change in number of people between the second and the fourth year.

\newline

(B) The time it took for the town to grow from a population of

2

people to a population of

4

\newline

(C) The number of people in the town on the fourth year.

\newline

(D) The average rate at which the population grew between the second and the fourth year.

Posted 7 months ago

Question

The cumulative profit a business has earned is changing at a rate of

r(t)

dollars per day (where

t

is the time in days). In the first

30

days, the business earned a cumulative profit of

\$ 1700

\newline

1700+\int_{30}^{90} r(t) d t

\newline

1

\newline

(A) The time it takes for the cumulative profit to increase another

\$ 1700

after the first

30

\newline

(B) The cumulative profit the business has earned as of day

90

\newline

(C) The rate at which the cumulative profit was increasing when

t=90

\newline

(D) The change in the cumulative profit between days

30

90

Posted 7 months ago

Question

A habitat of prairie dogs can support

m

\newline

The habitat's population,

p

, grows proportionally to the product of the current population and the difference between

m

p

\newline

Which equation describes this relationship?

\newline

1

\newline

\frac{d p}{d t}=k p(m-p)

\newline

\frac{d p}{d t}=\frac{k m}{m-p}

\newline

\frac{d p}{d t}=\frac{k p}{m-p}

\newline

\frac{d p}{d t}=k m(m-p)

Posted 7 months ago

Question

The amount of a particular pollutant

p

from a power plant in the air above the plant depends on the wind speed

s

, among other things, with the relationship between

p

s

approximated by

p=18-0.02s^{2}

s

in miles per hour.

\newline

a. Find the value(s) of

s

p=0

\newline

p=0

mean in this application?

\newline

c. What solution to

0=18-0.02s^{2}

makes sense in the context of this application?

Posted 6 months ago

Question

Seb bikes at a constant rate of

20

kilometers per hour.

1

. Write an equation that represents the distance, in kilometers, Seb travels

(b)

based on how many hours he bikes

(t)

2

. How far will Seb travel if he bikes at this rate for

3

\_

Posted 6 months ago

Question

\newline

\frac{1}{2}

\newline

\newline

\omega=\sqrt{\frac{k}{m}}

. This is the formula for the angular frequency

\newline

\omega

\newline

m

suspended from a spring of spring constant

\newline

k

. Solve this formula for

\newline

k

\newline

\newline

Posted 6 months ago

Question

Find the missing number so that the equation has no solutions.

\newline

-x - 17 - x = x + 1

Posted 1 hour ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant